arabera Amber Mohammad 3 years ago
423
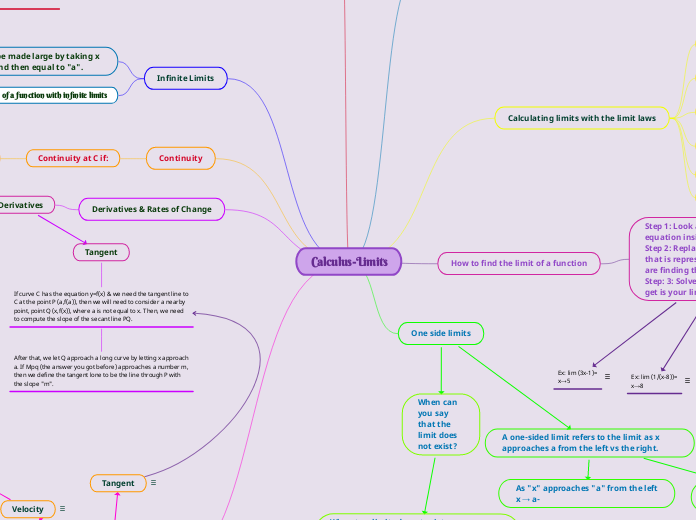
Calculus-Limits
arabera Amber Mohammad 3 years ago
423

Honelako gehiago
It is the displacement over time
The instantaneous velocity is the velocity at a specific time.
The average velocity is the distance travelled over a certain interval of time.
A tangent line is a line that touches a curve at one point.
If curve C has the equation y=f(x) & we need the tangent line to C at the point P (a,f(a)), then we will need to consider a nearby point, point Q (x,f(x)), where a is not equal to x. Then, we need to compute the slope of the secant line PQ.
After that, we let Q approach a long curve by letting x approach a. If Mpq (the answer you got before) approaches a number m, then we define the tangent lone to be the line through P with the slope "m".
In other words: A function is continuous if a small change in x produces a small change in f(x)
lim (x-1)/((x^2)-1)
lim (1/(x-8)) = ∞
x→8
(1/(x-8))
(1/(a-8))
(1/(8-8))
1/0
lim (3x-1) = 14
x→5
(3x-1)
(3(a)-1)
(3(5)-1)
(15-1)
14
lim f(x)=L; x->a
"L" - limit "a" - as "x" approaches (blank)
If f(x) doesn't exist as x approaches "a" from the left because the values of f(x) are becoming very large numbers (pos. or neg.) then we say lim x→a− f(x) = ∞ or -∞
If the above behavior happens when x approaches a from the right then we say lim x→a+ f(x) = ∞ or -∞
If both one-sided limits exhibit same behavior then we say lim x→a f(x) = ∞ or -∞
Moreover, in these cases the graph y = f(x) has a vertical asymptote at x = a.
You want to divide the numerator and denominator by the x with the highest exponent in f(x).
This is so that you can get rid of the x's. When you get fractions with x in the denominator, those turn into zero. When you solve, you will find your limit.
Ex: lim √(16x^(2)-8)/(2x-5)=2 x→∞
lim (√(16x^(2)-8))/(2x-5)=2
x→∞
lim (√(16x^(2)-8))/(2x-5) <---Divide the numerator and denominator by x (or multiply by (1/x)).
lim (√(16x^(2)-8)(1/x^2)/(2x-5(1/x^2)) =
x→∞
lim (√(16-(8/x)/(2-(5/x)) =
x→∞
lim (√(16-0))/(2-(0)) =
x→∞
lim (√(16x-0))/(2-(0)) =
x→∞
lim 4/2= 2
x→∞
The limit of f(x) as x approaches infinity is 2.
Ex: lim (1/x)=0 x→∞
lim (1/x) = 0
x→∞
(1/10)=.1
(1/100)=.01
1/1000)=.001
The answer gets smaller and smaller each time, and it gets closer to 0. So, you could say that the limit of (1/x) as x approaches infinity is zero.
lim (1/x) = +∞
x→0+
As you get closer to zero as you come from the right, you get closer to positive infinity.
lim (1/x)m= -∞
x→0-
As you get closer to zero as you come from the left, you get closer to negative infinity.