arabera Camila Sanchez 4 years ago
274
Metodo Post-Optimalidad y Sensibilidad
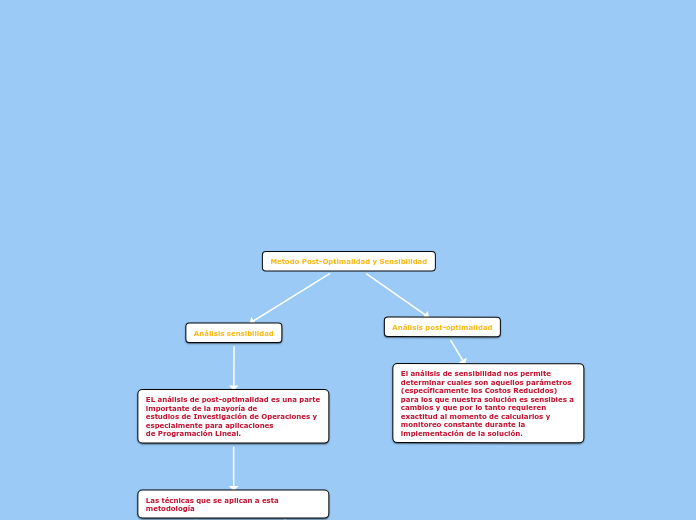
arabera Camila Sanchez 4 years ago
274

Honelako gehiago
Programación lineal paramétrica
Análisis de Sensibilidad
Precios Sombra
Re-optimización