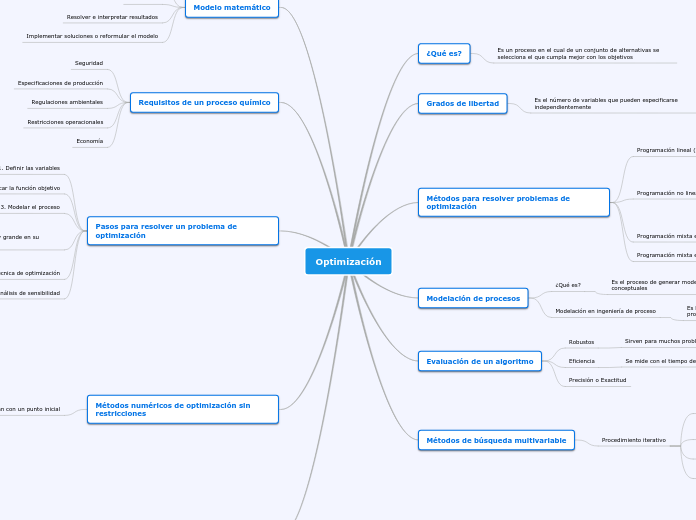
Optimización
Métodos de búsqueda unidimensional
b) Reducir el valor de f(x)
a) Calcular la dirección de búsqueda
Métodos numéricos de optimización sin restricciones
Son iterativos y comienzan con un punto inicial
Aproximaciones polinomiales
Se deben tener 3 puntos iniciales
Diferencias finitas
Es conveniente utilizarse cuando las funciones no están dadas por un modelo matemático o que la derivada esté muy compleja
x^k+1=x*k-((f(x+h)-f(x-h))/2h)/((f(x+h)-2f(x)+f(x-h))/h^2)
Quasi-Newton
Se deben tener dos puntos iniciales
m=(f'(xq)-f'(xp))/(xq-xp)
Newton
x^k+1=x^k-f'(x^k)/f''(x^k)
Desventajas
2. La convergencia es lenta
1. Cálculo de f'(x) y f''(x)
Ventajas
2. Para una función cuadrática el mínimo se obtiene en una nueva iteración
1. El algoritmo es cuadráticamente divergente
Grid Search
Pasos para resolver un problema de optimización
6. Análisis de sensibilidad
5. Aplicar una técnica de optimización
4. Si la acumulación del problema es muy grande en su alcance:
b) Simplificar la función objetivo y el modelo
a) Descomponer en partes manejables
3. Modelar el proceso
2. Especificar la función objetivo
1. Definir las variables
Requisitos de un proceso químico
Economía
Restricciones operacionales
Regulaciones ambientales
Especificaciones de producción
Seguridad
Modelo matemático
Implementar soluciones o reformular el modelo
Resolver e interpretar resultados
Modelación
Identificar el problema
Métodos de búsqueda multivariable
Procedimiento iterativo
4. Criterio de convergencia para la terminación
3. Especificar previamente los valores del punto inicial
2. Minimizar a lo largo de esa dirección para encontrar un nuevo punto
1. Escoger la dirección de búsqueda
Evaluación de un algoritmo
Precisión o Exactitud
Eficiencia
Se mide con el tiempo de computación/almacenamiento
Robustos
Sirven para muchos problemas
Modelación de procesos
Modelación en ingeniería de proceso
Es la representación matemática de un sistema físico para un proceso físico
Es el proceso de generar modelos matemáticos abstractos o conceptuales
Métodos para resolver problemas de optimización
Programación mixta entera no lineal (MINLP)
Outer Approximation
Programación mixta entera lineal (MILP)
Branch and Bound
Programación no lineal (NLP)
Gradiente reducido generalizado
Cuadrática
Secuencial
Programación lineal (LP)
Simplex
Grados de libertad
Es el número de variables que pueden especificarse independientemente
Nf=Nv-Ne
Ne=Número de ecuaciones independientes
Nv=Número total de ecuaciones
Nf=Número de grados de libertad
¿Qué es?
Es un proceso en el cual de un conjunto de alternativas se selecciona el que cumpla mejor con los objetivos