jonka Ronald Báez Gómez 5 vuotta sitten
918
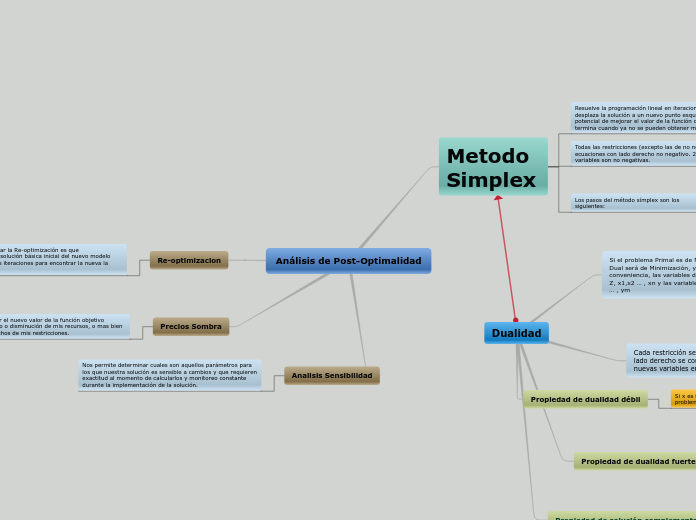
Análisis de Post-Optimalidad
El análisis de post-optimalidad permite evaluar cómo las variaciones en los recursos afectan el valor de la función objetivo. El análisis de sensibilidad identifica los parámetros críticos cuya variación influye en la solución y requieren un monitoreo constante.