Can inequalities be like equations?
Inequalities
Complex: x/3*7-15≤127
Complex: x/5*17-34≤4/2*8-35+169
One Step: x+3≥10
Two Step: x/3+8≤15
Inequalities can be like equations and this relation would be the fact that one/two step inequalities exist. This meaning that complex inequalities also exist and we can solve all of these just like we would solve normal equations except for the fact that we have to work with an inequality sign instead of an equal sign.
x > 2
An inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size.
Wait, why are there sentences in math?
Sentences
Number Sentence
To sum it up, a number sentence is a statement of equality or inequality between two numerical expressions.
A number sentence does not always have to be true but, it does have criteria to be considered a number sentence. These would be numbers, at least one mathematical operation, equal or inequality sign, and a number after said sign.
Algebraic Sentance
a^2=9
K–M>6
4a=8
An algebraic sentance is just a number sentance with one or more variable involved in the sentence
These are not the same as a sentence in language arts, because of the fact that there are two types of theme, number and algebraic sentences.
What would you call an equation with 3 steps or what about 5?
What are these type of equations?
What are the other definitions of an equal sign?
So they are just supposed to show the answer in them?
Why do you need to know how to evaluate expressions/equations?
How are expressions related to the Complex Number System?
Why are there two different types of expressions?
What is an expression?
Expressions
Evaluating Expressions/Equations
Equations are the complete opposite of expressions because of the fact that they are supposed to have equal signs in them.
One/Two Step equations
One step equations quite literally define themselves since they are equations that only need one step to solve.
Two step equations are when it gets a little trickier because of the fact that they require two steps to solve completely.
An equation with 3 steps or more is called a complex equation and to solve these you need to have mastered one/two step equations because they build on them exponentially depending on how many steps they have.
x+8-2=10
x*2+4=26
x+5=15
x-27=2
Equation: 2+3=5
Expression: 5+4*2
I am not that advanced to know what they all are, but I do know two of them which would be a calculation or an equivalance statement.
Calculation:2+4+5=11
Equivalence statement: 2+4=5+1
Kind of, and I say this because of the fact that an answer is one of the ways an equal sign is known for, but there are other definitions of the equal sign.
You need to know how to evaluate them because of the fact that they can also be put on a coordinate plane along with the fact that they are roots to what we will be evaluating in later units/classes.
Expressions are related to the complex number system because of the fact that they consist of thing that are in or related to the system.
Variables, Numbers, Operations
Numerical Expressions
2+5
A numerical expression is just an expression with no variables and one or more numbers.
Algebraic Expressions
2x+4
An algebraic expression is an expression with one or more variables in it.
An expression is a statement that does not contain an equal sign but, it needs to have at least more than 1 number and an operation.
2+1
There are also two different types of expressions.
This is because of the fact that there are a slight difference between the two so we need to seperate them for ordering reasons.
Unit 1
Unit 2
Sheraz Fayyaz P.2
Can you estimate other roots as well?
Other roots can also be estimated using the method but square roots are mentioned because they are the most used root and the one that usually occur the most.
Imaginary numbers can also be used in things called quadratic equations. How this works is that when you are evaluating a quadratic equation, if you end up with a negative value under the square root, you end up creating an imaginary number. Lastly, imaginary numbers can be used in other things, but electricity and quadratic equations are the two main things that they are associated with.
Can imaginary numbers be used in other topics that are not related to electricity?
Lastly, the closure property is also connected to algebraic and numerical expressions which is another link that it has with the other topics of the complex number system.
Lastly, square roots are also related to the imaginary part of the system because they can also be used with imaginary numbers. An example of this could be in my previous remarks about electricity or in the quadratic equations I also mentioned.
These are numbers without fractions and they have no negative numbers.
Like whole numbers they are numbers
with fractions but, they also include
there negative counterparts.
Why are rules important in scientific notation?
Rules are important for exponents because of the fact that they keep exponents in order. An example of this could be how the product rule tells you to add exponents while the power to product rule tells you to multiply them.
Legend:
Bold: Main Topic
Main Topic: Orange
Topics: Yellow
Questions:Red
Question Answers: Light Blue
Rules: Purple
Examples: Dark Blue
Explanations: Green
So why is it not under the Complex Number System section?
The closure property is mainly for the Complex Number System since it helps determine what numbers stay in their own set.
The reason that the closure property is still here is because of the fact that it applies to other topics such as square roots and exponents.
This all connects to the four operations because of the fact that we use/ can use the four operations in all of these topics and they are a fundamental part of our entire world.
Square roots are also related to rational and irrational numbers because of the fact that perfect squares are rational number while every other square root ends up being an irrational number.
Square roots are related to the complex number system because of the fact that like exponents, they have a base foundation of numbers from the system and do something to numbers. But unlike the exponents, they do the complete opposite which is splitting a number into its square or whatever number is on the outside of the sign, which is also a difference from exponents.
Estimating square roots is important because of the fact that it allows you to give a close guess as to what the square root of a number it since every square root of a number that is not a perfect square is irrational, so we at least need to get a sense for how big these square roots are.
Why is estimating square roots important?
How are square roots related to the Complex Number System?
Why is the Closure property down here and also related to everything?
Why does this all connected to the 4 operations?
The reason that rules in Scientific Notation are important is because if the fact that we can understand it with them and so everyone is using the same ways to write it. If everyone had their own interpretation of them we would get very confused when working with very large or small numbers.
Why does simplification even need to be mentioned in this concept map?
Why do we use scientific notation?
Since we already know what an exponent is and how its related, why do we need to have rules for them?
How are exponents related to the Complex Number System?
Can zero be a Natural Number?
How are they used in electricity?
4 Operations
Closure Property
Methods of Simplification
Simplification is labeled because of the fact that simplification is a huge part in math and keeps it orderly. The reason it applies to these topics is because of the fact that they can all be used to simplify a number in different ways.
Square Roots
Cube Roots
Perfect Squares and Perfect Cubes
Imperfect Squares and Cubes
Estimating Square Roots
Prime Factorization
Prime factorization is just a method in which you factor down a number to its lowest numbers, it can also be related to square roots because of the fact that it is used to evaluate square roots sometimes.
This does not just stop at roots, prime factorization can be a huge fundamental in higher math because of its simplicity and usefulness.
Lastly, this topic expands to many lengths like prime decomposition and the different types of primes there are in math. Of course we will probably not learn these things in a long time.
Used To Simplify Numbers
Can be used on Square Roots
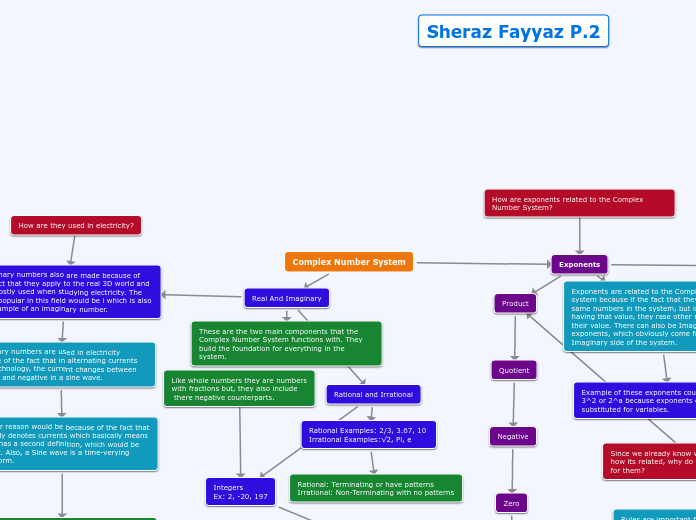
Complex Number System
Exponents
Product
Quotient
Negative
Zero
Power to Product
Exponents are related to the Complex Number system because if the fact that they are the same numbers in the system, but instead of just having that value, they rase other numbers to their value. There can also be Imaginary exponents, which obviously come from the Imaginary side of the system.
Example of these exponents could be
3^2 or 2^a because exponents can also be substituted for variables.
Scientific Notation
We use scientific notation because of the fact that it is an appropriate system of simplification that allows us to work with very small or large numbers much more easily than doing anything with them regularly.
Rules
Base of 10
Number between 1-9
Real And Imaginary
Imaginary numbers also are made because of the fact that they apply to the real 3D world and are mostly used when studying electricity. The most popular in this field would be i which is also an example of an imaginary number.
Imaginary numbers are used in electricity because of the fact that in alternating currents (AC) technology, the current changes between positive and negative in a sine wave.
Another reason would be because of the fact that i already denotes currents which basically means that it has a second definition, which would be current. Also, a Sine wave is a time-verying wave form.
The reason the any of this is important is because of the fact that doing calculation with AC currents is very hard and this will help people that work with them stay shock-free.
These are the two main components that the Complex Number System functions with. They build the foundation for everything in the system.
Rational and Irrational
Rational Examples: 2/3, 3.67, 10
Irrational Examples:√2, Pi, e
Rational: Terminating or have patterns
Irrational: Non-Terminating with no patterns
Integers
Ex: 2, -20, 197
Whole
Ex: 2, 6, 987
Natural
Ex: 1, 2, 3
These are also referred to as counting numbers.
Zero can be a natural number, but it mostly depends on the mathematician because of the facts that different field in math teach different things so, it is debated.