jonka Zharick Herrera 3 vuotta sitten
245
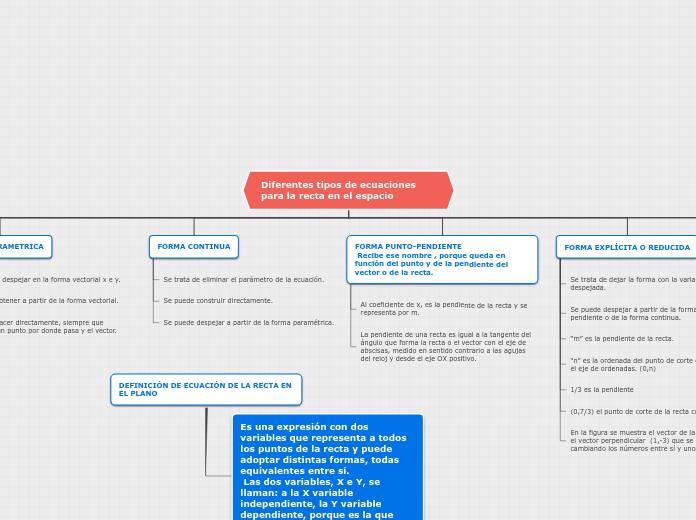
Diferentes tipos de ecuaciones para la recta en el espacio
Una ecuación de la recta en el plano es una expresión matemática con dos variables que representa todos los puntos de una recta. Las variables, X e Y, se denominan respectivamente independiente y dependiente.