jonka Etienne jerry dukens 3 vuotta sitten
360
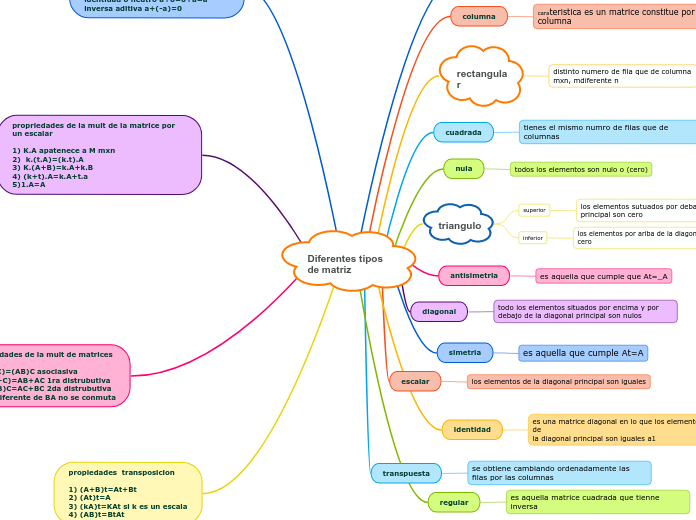
Diferentes tipos de matriz
Una matriz transpuesta se obtiene al intercambiar filas por columnas. Las matrices pueden ser de diferentes tipos: cuadradas, rectangulares, nulas, diagonales, entre otras. La matriz cuadrada tiene el mismo número de filas y columnas, mientras que la rectangular tiene diferente número de filas y columnas.