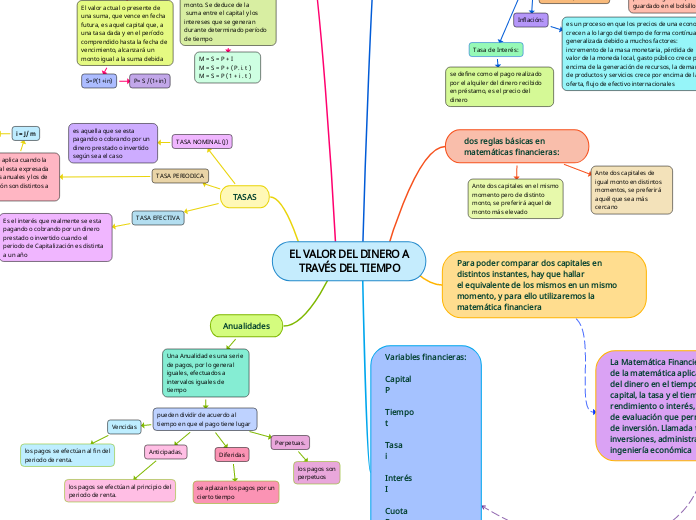
La Matemática Financiera es una derivación de la matemática aplicada que estudia el valor del dinero en el tiempo, combinando el capital, la tasa y el tiempo para obtener un rendimiento o interés, a través de métodos de evaluación que permiten tomar decisiones de inversión. Llamada también análisis de inversiones, administración de inversiones o ingeniería económica
factor principal en el cambio del valor del dinero a través
EL VALOR DEL DINERO A TRAVÉS DEL TIEMPO
Anualidades
Una Anualidad es una serie de pagos, por lo general
iguales, efectuados a intervalos iguales de tiempo
pueden dividir de acuerdo al tiempo en que el pago tiene lugar
Perpetuas.
los pagos son
perpetuos
Diferidas
se aplazan los pagos por un
cierto tiempo
Anticipadas,
los pagos se efectúan al principio del
periodo de renta.
Vencidas
los pagos se efectúan al fin del
periodo de renta.
TASAS
TASA EFECTIVA
Es el interés que realmente se esta pagando o cobrando por un dinero prestado o invertido cuando el periodo de Capitalización es distinta a un año
r = (1 + i )^m -1
TASA PERIODICA
tasa que se aplica cuando la tasa nominal esta expresada
en términos anuales y los de Capitalización son distintos a un año
i = J/ m
m: numero de Capitalizaciones en un año
TASA NOMINAL (J)
es aquella que se esta pagando o cobrando por un dinero prestado o invertido según sea el caso
INTERESES
INTERÉS COMPUESTO
Valor Presente
P = S/(1 + i )^n
Valor Futuro
S = P (1 + i )^n
Es el interés que se genera sobre intereses. Los intereses que se generan en el primer periodo de capitalización se convierten en capital para generar mas intereses para el segundo periodo de capitalización y así sucesivamente
INTERÉS SIMPLE
Valor Presente Simple
El valor actual o presente de una suma, que vence en fecha
futura, es aquel capital que, a una tasa dada y en el período
comprendido hasta la fecha de vencimiento, alcanzará un
monto igual a la suma debida
S=P(1+in)
P= S /(1+in)
Valor futuro a interés simple
Tambien conocido como monto. Se deduce de la
suma entre el capital y los intereses que se generan durante determinado período de tiempo
M = S = P + I
M = S = P + ( P. i. t ) M = S = P ( 1 + i . t )
Es aquel interes que se genera sobre un capital que permanece constante en el tiempo
i = I / P I = P. i. t
Variables financieras:
Capital
P
Tiempo
t
Tasa
i
Interés
I
Cuota
R
Monto (Valor Futuro)
M (S)
Valor Presente
P (A)
Para poder comparar dos capitales en distintos instantes, hay que hallar
el equivalente de los mismos en un mismo momento, y para ello utilizaremos la matemática financiera
dos reglas básicas en matemáticas financieras:
Ante dos capitales en el mismo momento pero de distinto monto, se preferirá aquel de monto más elevado
Ante dos capitales de igual monto en distintos momentos, se preferirá aquél que sea más cercano
El factor tiempo juega un papel decisivo a la hora de fijar el valor de un
capital
resultado de la interacción de factores como el el costo de oportunidad y la inflación
Tasa de Interés:
se define como el pago realizado por el alquiler del dinero recibido en préstamo, es el precio del dinero
Inflación:
es un proceso en que los precios de una economía crecen a lo largo del tiempo de forma contínua y generalizada debido a muchos factores: incremento de la masa monetaria, pérdida de valor de la moneda local, gasto público crece por encima de la generación de recursos, la demanda de productos y servicios crece por encima de la oferta, flujo de efectivo internacionales
Costo de oportunidad:
sacrificio en el que se incurre al tomar una decisión. El dinero puede ser destinado a distintas actividades: puede ser gastado, invertido o simplemente guardado en el bolsillo
No es lo mismo disponer de $ 1 millón hoy que dentro de un año