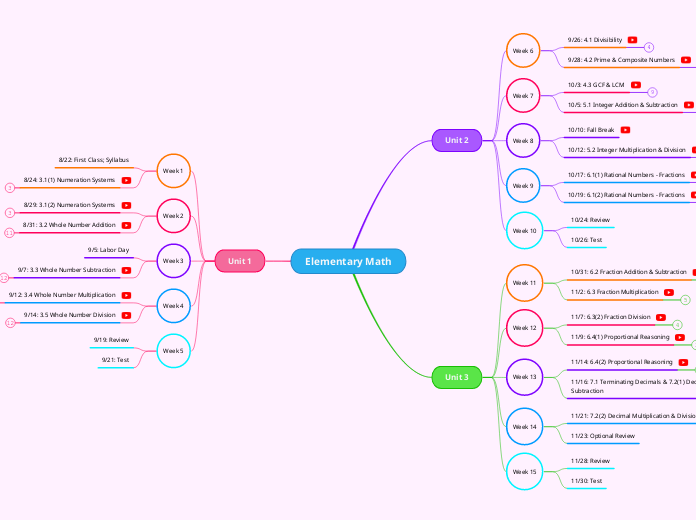
Elementary Math
Unit 1
Week 5
9/21: Test
9/19: Review
Week 4
9/14: 3.5 Whole Number Division
Order of Operations
Order of operations states that when no parentheses are present, multiplications and divisions are performed before additions and subtractions (from left-to-right).
ex: 8-9/3*2+3
8-9/3*2+3 = 8-3*2+3
= 8-6+3
= 2+3
= 5
Computational estimation may help determine if an answer is reasonable. Strategies include:
- Compatible numbers
ex:
_____ ______ 800
5 |4163 5 |4000 5 |4000
Mental computation strategies include the following algorithms:
1 - Breaking up the dividend
ex:
______
7 |4256
_______
7 |42|56
600+ 8
7 |4200+56
600+8=608
2 - Using compatible numbers
ex:
_____
3 |105 105=90+15
30+ 5
3 |90+15 105/3=35
Partial-Quotients (Scaffold) Algorithm
The partial-quotients algorithm uses the repeated subtraction approach, where partial quotients are written next to the problem. Scaffolding is utilized to show place value prior to achieving the standard algorithm.
ex:
______
32 |4224
-3200 (100*32)
1024
- 960 (30*32)
64
- 64 (2*32)
0 132*32
Using Base-Ten Blocks to Develop the Standard Division Algorithm
Using base-ten blocks to develop the standard division algorithm involves starting with a concrete model, then moving to the standard algorithm.
ex: 726/6
121
6 |726
-6
12
-12
6
-6
0
Relating Multiplication and Division as Inverse Operations
Division with remainder zero is the inverse of multiplication, similar to how subtraction is the inverse of addition. In addition to this, repeated subtraction is the inverse of repeated addition.
ex: 6*5=30 5*6=30 30/5=6 30/6=5
Division by 0 and 1
Division by 0 follows 3 rules:
- n/0 is undefined.
- 0/n is 0.
- 0/0 is undefined.
ex:
3/0 = undefined
0/3 = 0
Division by 1 follows the definition of division:
- n/1=n
ex:
3/1 = 3
1/1 = 1
0/1 = 0
The Division Algorithm
The division algorithm states that given any whole numbers a and b with b=/=0, there exist unique whole numbers q (quotient) and r (remainder) such that a=bq+r with 0<=r<b.
ex: 32/6 q=5 r=2
32=6*5+2 with 0<=2<6
Whole Number Division Properties
Whole number division properties include none since the set of whole numbers is not closed under division.
ex: 27/5 5c=27
No whole number c satisfies this equation; 27/5 has no meaning in the set of whole numbers.
Missing-Factor Model
The missing-factor model states that for any whole numbers a and b, with b=/=0, a/b=c if, and only if, c is the unique whole number such that b*c=a.
ex: 18 cookies to share between 3 friends
If each friend receives c cookies, then the 3 friends receive 3c, or 18, cookies; 3c=18; because 3*6=18, c=6.
Set (Partition) Model
The set (partition) model is for finding an unknown group's size.
ex: 18 cookies to share between 3 friends
18
OOOOOOOOO
OOOOOOOOO
OOOOOO OOOOOO OOOOOO
6 6 6
18/3=6
Repeated-Subtraction Model
The repeated-subtraction model is for finding an unknown number of groups.
ex: 18 cookies, X packages hold 6 cookies each
18-6=12 18-6-6-6=0 18/6=3
12-6=6
6-6=0
9/12: 3.4 Whole Number Multiplication
Computational estimation may help determine if an answer is reasonable. Strategies include:
- Front-end ex: 524*8 500*8=4000 20*8=160 4000+160=4160
- Compatible numbers ex: 524*8 500*8=4000 25*8=200 4000+200=4200
Mental computation strategies include the following algorithms:
- Front-end multiplying ex: 64*5 60*5=300 4*5=20 300+20=320
- Using compatible numbers ex: 2*9*5*20*5 9*(2*5)*(20*5) = 9*10*100 = 9000
- Thinking money ex: 64*5 64 nickels=32 dimes 32*10=320
Multiplication in Bases Other than Ten
Multiplication in bases other than ten is simple since multiplication facts for other bases can be derived using the repeated addition model.
ex:
Base Five Multiplication Table
x 0 1 2 3 4
0 0 0 0 0 0
1 0 1 2 3 4
2 0 2 4 11 13
3 0 3 11 14 22
4 0 4 13 22 31
There are several ways to solve equations in other bases, including using expanded, partial-products, lattice, and standard models.
ex: 21(five)*3(five)
(20+1)(five)
* 3(five)
(110+3)(five)
Lattice Multiplication
Lattice multiplication delays all additions until all single-digit multiplications have been completed.
ex: 14*23
1 4
|0/|0/|2
|/2|/8|
|0/|1/|3
3 |/3|/2|
2 2 = 322
Partial-Products Algorithm
The partial-products algorithm is performed by first considering place value, then expanded notation and computing all partial products, one place value at a time, lastly adding all partial products together.
ex: 14*23
Expanded notation:
23
*14
200 (10*20)
30 (10*3)
80 (4*20)
+12 (4*3)
322 (200+30+80+12)
Partial-products algorithm:
23
*14
92 (4*23)
230 (10*23)
322
Using Base-Ten Blocks to Develop the Standard Multiplication Algorithm
Using base-ten blocks to develop the standard algorithm for whole number multiplication involves starting with a concrete model, then moving to the expanded algorithm, and last to the standard algorithm.
ex: 4*12
Concrete model (with repeated addition):
( l .. ) ( l .. ) ( l .. ) ( l .. )
( l l l l )
( ........ )
4*12=48
Expanded model:
10+2
* 4
40+8 = 48
Standard model:
12
*4
48
Whole Number Multiplication Properties
Whole number multiplication properties include:
Closure property of multiplication of whole numbers - for whole numbers a and b, a*b is a unique whole number.
ex: 2*3=6
Commutative property of multiplication of whole numbers - for whole numbers a and b, a*b=b*a.
ex: 6*4=4*6
Associative property of multiplication of whole numbers - for whole numbers a, b, and c, (a*b)*c=a*(b*c).
ex: (3*5)*2=(5*2)*3
Identity property of multiplication of whole numbers - there is a unique whole number 1, the multiplicative identity, such that for every whole number a, a*1=a=1*a.
ex: 3*1=3=1*3
Multiplication property of zero for whole numbers - for every whole number a, a*0=0=0*a.
ex: 6*0=0=0*6
Distributive property of multiplication over addition for whole numbers - for whole numbers a, b, and c, a(b+c)=ab+ac.
ex: 8(5+2)=(8*5)+(8*2)
Distributive property of multiplication over subtraction for whole numbers - for whole numbers a, b, and c with b>=c, a(b-c)=ab-ac.
ex: 8(5-2)=(8*5)-(8*2)
Cartesian-Product Model
The Cartesian-product model is portrayed as a tree diagram or a table, showing all possible combinations of items. Each set may be written as an ordered pair, forming the Cartesian product B*C. For finite sets A and B, if n(A)=a and n(B)=b, then a*b=n(A*B). A*B indicates the Cartesian product; numbers are multiplied & sets are not.
ex:
Condiment
B | m c h
r |d | dm dc dh
e | l | lm lc lh
a |
d |
Rectangular-Array and Area Models
An array is used in multiplication when objects are arranged with the same numbers of objects in each row and column.
ex: OOOO
OOOO
OOOO
In an area model, lines cross to form intersection points, forming an array of points, or a grid.
ex: ╋ ╋ ╋ ╋ ╋ ╋
╋ ╋ ╋ ╋ ╋ ╋
╋ ╋ ╋ ╋ ╋ ╋
╋ ╋ ╋ ╋ ╋ ╋
╋ ╋ ╋ ╋ ╋ ╋
Repeated Addition Model
The repeated addition model can be used when equal-sized groups are being put together.
ex: 3 groups of 8 goldfish
8+8+8=24
^-----^
3
8 * 3 = 24
<--------------------------------------------->
8 8 8
<---------><-------------><---------------->
<-0-2-4-6-8-10-12-14-16-18-20-22-24->
Week 3
9/7: 3.3 Whole Number Subtraction
Mental computation strategies help produce an answer without manipulatives and facilitate in approximating or estimating the answer to a problem. Consider several algorithms for mental computation:
- Breaking up and bridging ex: 67-36 67-30=37 37-6=31
- Trading off ex: 71-39 71+1=72 39+1=40 72-40=32
- Drop the zeros ex: 8700-500 87-5=82 82-->8200
Understanding Subtraction in Bases Other than Ten
Understanding subtraction in bases other than ten is simple since subtraction facts for other bases can be derived using the definition of subtraction.
ex: 12(five)-4(five)=c if c+4(five)=12(five)
The equal-additions algorithm and other algorithms used in base-ten equations can be used in other bases, as well.
ex: 432(five)-43(five)
432(five) 432(five)+2 434(five)
- 43(five) --> - (43(five)+2) --> - 100(five)
334(five)
Trades-First Algorithm
The trades-first algorithm is similar to the standard algorithm, except all regrouping is done first, prior to any subtraction is performed.
ex: 122-37
hundreds tens ones
1 2 2
12 2
11 12
-- 3 7
8 5
Counting-Up Algorithm
The counting-up algorithm is also known as the "making change" method. It is performed using mental math and is based on the missing addend model.
ex: 100-31
31+ [9] =40
40+ [60] =100
9+60=69
Equal Additions Algorithm
The equal additions algorithm is based on the fact that the difference between two numbers does not change if we add the same amount to both numbers.
ex:
93-27 = (93+3) - (27+3) --> 96-30=66
Using Base-Ten Blocks to Develop the Standard Subtraction Algorithm
Using base-ten blocks to develop the standard algorithm for whole number subtraction involves starting with a concrete model with trading, then moving to the expanded algorithm with trading, and last to the standard algorithm with regrouping.
ex: 243-61
Concrete model:
243: ▦ ▦ llll ...
trading: ▦ --> lllll lllll
▦ llll ...
243-61: ▦ lllll lll (ll llll) .. (.)
182: ▦ lllll lll ..
Expanded model:
2*10^2+4*10+3 1*10^2+14*10+3
- (6*10+1) --> - (6*10+1)
1*10^2+(14-6)10+(3-1)
= 1*10^2+8*10+2
= 182
Standard model:
243
- 61
182
Using Whole Number Addition and Subtraction in Equations
Using whole number addition and subtraction in equations requires that a value which makes an equation true be a solution to that equation.
ex:
9+5=O and 12-O=4 <-true/false depending on the value of O.
Whole Number Subtraction Properties
Whole number subtraction properties include none since the set of whole numbers is not closed under subtraction; if a<b, then a-b is not meaningful in the set of whole numbers.
ex: 5-3=2 3-5=-2
The comparison model is used by determining how many more a is than b.
ex: 8-3=5
8
OOOOOOOO
OOO ^-------^
3 5
Missing Addend Model
The missing addend model relates addition and subtraction; for any whole numbers a and b such that a>=b, a-b is the unique whole number c such that b+c=a.
ex: 8-3=?
3+[8-3]=8
8-3=5 is the missing addend.
The number line (measurement) model entails subtraction of whole numbers modeled on a number line using directed arrows.
ex: 5-3=2
3 2
<------><-->
5
<------------>
<-0-1-2-3-4-5->
Take-Away Model
The take-away model is when a subset is being taken away from a primary set.
ex:
8 cookies
OOO (O) --> take away 2
OOO (O) 8-2=6 cookies left
9/5: Labor Day
Week 2
8/31: 3.2 Whole Number Addition
Computational estimation is the process of forming an approximate answer to a numerical problem. It may help determine if an answer is reasonable. Strategies include:
- Front-end with adjustment ex: 423+338+561 4+3+5=12 hundred 61+38=100 100+20=120 1200+120=1320
- Grouping to nice numbers ex: 23+39+32+64+49 39+64=100 23+32+49=100 100+100=200
- Clustering ex: 6200+5842+6512+5521+6319 5*6000=30,000
- Rounding ex: 4274+3192 5000+3000=8000
- Using the range ex: 378+524 low: 300+500=800 high: 400+600=1000 range: 800-1000
Mental computation is the process of producing an answer to a computation without using physical computation aids. Consider several algorithms for mental computation:
- Adding from the left ex: 67+36 60+30=90 7+6=13 90+13=103
- Breaking up and bridging ex: 67+36 67+30=97 97+6=103
- Trading off ex: 67+36 67+3=70 36-3=33 70+33=103
- Using compatible numbers ex: 130+50+70+20+50 130+70=200 50+50=100 100+200=300 300+20=320
- Making compatible numbers ex: 25+79 25+75=100 100+4=104
Understanding Addition in Bases Other than Ten
Understanding addition in bases other than ten is necessary as it provides valuable insight into computation in base ten. The use of multibase blocks aids in this understanding and building an addition table for different bases.
ex:
Base Five Addition Table
+ 0 1 2 3 4
0 0 1 2 3 4
1 1 2 3 4 10
2 2 3 4 10 11
3 3 4 10 11 12
4 4 10 11 12 13
Opposite-Change Algorithm
In the opposite-change algorithm, the goal is to make the addition problem a problem without the need to regroup.
ex: 189+278
+1 +10
189 ---> 190 ----> 200
-1 -10
278 ---> 277 ----> +267
467
Lattice Algorithm
In the lattice algorithm, single-digit numbers on top are added by place value to the single-digit numbers on bottom, and the results are recorded in a lattice. Then, the sums are added along the diagonals and written along the bottom.
ex:
3 5 6 7
+ 5 6 7 8
|0/|1/|1/|1/|
|/8|/1|/3|/5|
9 2 4 5
Partial-Sums Algorithm
In the partial-sums algorithm, one must first compute all sums, one place value at a time, then add all partial sums to find the total sum. This algorithm emphasizes place value.
ex:
568
+757
1200 (500+700)
110 (60+50)
+ 15 (8+7)
1325
Using Base-Ten Blocks to Develop the Standard Algorithm
Using base-ten blocks to develop the standard algorithm for whole number addition involves starting with a concrete model, then moving to the expanded algorithm, and last to the standard algorithm.
ex: 14+23
Concrete model:
14: l .... 23: ll ...
lll .......
14+23=37
Expanded model:
14
+23
7
+30
37
Standard model:
14
+23
37
Whole Number Addition Properties
Whole number addition properties include:
Closure property of addition of whole numbers - if a and b are whole numbers, then a+b is a unique whole number.
ex: 5+2=7
Commutative property of addition of whole numbers - if a and b are any whole numbers, then a+b=b+a.
ex: 2+9=9+2
Associative property of addition of whole numbers - if a, b, and c are any whole numbers, then (a+b)+c=a+(b+c).
ex: (24+8)+2=24+(8+2)
Identity property of addition of whole numbers - for any whole number a, a+0=a=0+a.
ex: 5+0=5=0+5
Mastering Basic Addition Facts
Mastering basic addition facts strategies include:
- Counting on ex: 5+3 -> 6, 7, 8
- Doubles ex: 3+3 (doubles + 1, doubles + 2)
- Making 10 ex: 9+8 -> (9+1)+7 -> 10+7 -> 17
Number Line (Measurement) Model
A number line is another way of modeling whole number addition. It at least consists of a line marked with two points, 0 and 1.
ex:
4 + 3 = 7
<----------------->
4 3
<---------><----->
<-0-1-2-3-4-5-6-7->
A set model is one way of representing whole number addition.
ex:
n(A) = 4 n(B) = 3
A: OO B: OO
OO O
A+B: OOOO
OOO
n(A+B) = 7
8/29: 3.1(2) Numeration Systems
Base Twelve
Base twelve is also called the duodecimal (dozens) system. It has 12 digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, T, and E.
ex: 19, 1T, 1E, 20,..., 29, 2T, 2E, 30,...
Base Two
Base two was used by early tribes and by some aboriginal tribes still today. It is called the binary system because it has only two digits, 0 and 1.
ex: 2^4 = 16, 2^3 = 8, 2^2 = 4, 2^1 = 2, 2^0 = 1
Base Five
Base five was used by the Luo peoples of Kenya and was referred to as the quinary system. The counting digits included: 0, 1, 2, 3, and 4. Usage of the subscript five is vital, because if no base is written, a numeral is assumed to be in base-ten.
Base five blocks:
1 block = 125 units
1 flat = 25 units
1 long = 5 units
1 unit = 1 unit
ex: 34(five) + 1 = 40(five)
Week 1
8/24: 3.1(1) Numeration Systems
Hindu-Arabic Numeration System
Hindu-Arabic Numeration System was developed by the Hindus and transported to Europe by the Arabs. It relies on the following two properties:
- All numerals are constructed from 10 digits--0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
- Place value is based on powers of 10, the number base of the system.
Because it is based on powers of 10, it is called a base-ten or decimal system.
ex: 65,984
6 - ten thousand = 60,000 (10^4)
5 - thousand = 5,000 (10^3)
9 - hundred = 900 (10^2)
8 - ten = 80 (10^1)
4 - one = 4 (1)
Mayan Numeration System
Mayan numeration system used only 3 symbols, representing numbers 0, 1, and 5. They were the first to introduce a symbol for zero.
ex: 1, 20, 20*18, 20^2*18, 20^3*18
Numerals
Numerals are defined as figures, symbols, or a group of these denoting a number.
ex: 2 or 5
8/22: First Class; Syllabus
Unit 3
Week 15
11/30: Test
11/28: Review
Week 14
11/23: Optional Review
11/21: 7.2(2) Decimal Multiplication & Division
"How Many Groups?" Method
The "how many groups?" method is done by counting how many groups there are and finding the unknown number of groups.
Outline 0.27 and color groups of 0.04. Then end up with six groups of 0.04 and a remainder of 0.03. Since 0.04 is four hundredths shaded and there are three hundredths remaining in 0.27, three out of four fit, or 0.03 out of a group of 0.04 fit;
0.03 out of 0.04 = (0.03/0.04) * (100/100) = ¾ = 0.75
0.27 / 0.04 = 6.75
Partition (Equal Groups) Method
The partition (equal groups) method is done by dividing a number into equal groups and finding the unknown group size.
ex: 0.54 / 3 = 0.18
Outline 0.54 and then divide the columns (tenths) into three equal groups and each group has one tenth. Then divide the remaining squares (twenty-four hundredths) into three equal groups and each group has 8 hundredths. Each group uses exactly eighteen squares, so 0.54 / 3 = 0.18.
Using Estimation to Place Decimal Point
To use estimation in placing the decimal point, ignore the decimal points and do the multiplication or division as if all numbers were whole numbers. When finished, place the decimal point in the result by estimation.
ex: 8.2 * 2.63 = 21.566
263
x 82
21566 8 * 2 = 16 8 * 3 = 24
Multiplying Decimals Algorithm
The multiplying decimals algorithm is as follows: if there are n digits to the right of the decimal point in one number and m digits to the right of the decimal point in a second number, multiply the two numbers, ignoring the decimals, and then place the decimal point so that there are n+m digits to the right of the decimal point in the product.
ex: 4.62 * 2.4 = 11.088
462
x 24
11088
Week 13
11/16: 7.1 Terminating Decimals & 7.2(1) Decimal Addition & Subtraction
Rounding Decimals
Rounding decimals is possible when it is not necessary to know the exact answer.
ex: 7.456 to the nearest hundredth = 7.46
7.456 to the nearest tenth = 7.5
7.456 to the nearest unit = 7
7456 to the nearest thousand = 7000
745 to the nearest ten = 750
74.56 to the nearest ten = 70
Mental Computation
Some tools used for mentally computing whole numbers may also work with rational numbers.
ex:
- Breaking and bridging: 1.5 + 3.7 + 4.48
⎝ ⎠
4.5 + 0.7 + 4.48
⎝ ⎠
5.2 + 4.48
⎝ ⎠
9.2 + 0.48 = 9.68
- Using compatible numbers: 7.91 ⎯ 12
4.09___⎠
3.85 ⎯ + 4
+ 0.15 _⎠16
⎯⎯⎯
- Making compatible numbers: 9.27 = 9.25 + 0.02
+ 3.27 = 3.75 + 0.04
13.00+0.06=13.06
- Balancing with decimals in subtraction: 4.63
- 1.97 or...
4.63 + 0.03 = 4.66
- (1.97 + 0.03) = - 2.00
2.66
Adding & Subtracting Decimals by Writing as Fractions
To add and subtract decimals, change the problem to one that's easier to solve, by writing it as a sum of fractions.
ex: 2.16 + 1.73 = (2 + 1⁄10 + 6⁄100) + (1 + 7⁄10 + 3⁄100)
= (2 + 1) + (1⁄10 + 7⁄10) + (6⁄100 + 3⁄100)
= 3 + 8⁄10 + 9⁄100
= 3.89
Adding & Subtracting Decimals Using Base-Ten Blocks
To add and subtract decimals using base-ten blocks, one must state what they are using for their whole.
ex: 1 flat = 1 whole
▦▦ l ......
2 1⁄10 6⁄100 = 2.16
▦ lllllll ...
1 7⁄10 3⁄100 = + 1.73
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
▦▦▦ llllllll .........
3 8⁄10 9⁄100 = 3.89
Terminating Decimals
A terminating decimal is a number that can be written with a finite number of places to the right of the decimal point.
A rational number a/b in simplest form can be written as a terminating decimal if, and only if, the prime factorization of the denominator contains no primes other than 2 or 5.
ex: Is 7⁄8 a terminating decimal?
Yes, since 8 has 2^3 as its only factor.
ex: Is 8⁄14 a terminating decimal?
No, since 14 has factors 2 and 7.
11/14: 6.4(2) Proportional Reasoning
Scale
Scale is the ratio of the size of the drawing to the size of the object.
ex: if the scale is 1:300, then 1 cm represents 300 cm or 3 m
Unit Rate Strategy
The unit rate strategy is a strategy for solving proportions by identifying and using the constant of proportionality.
ex: 12 tickets for $15 (1 ticket = $1.25)
20 tickets for $23 (1 ticket = $1.15)
Constant of Proportionality
If the variables x and y are related by the equality y = kx (or k = y / x), then y is proportional to x and k is the constant of proportionality between y and x.
ex: 1⁄20 = 2⁄40 = 3⁄60 = 4⁄80
^ 1⁄20 is the constant of proportionality for the above ratios
Multiplicative Relationships
A multiplicative relationship is when a problem presents a proportion which may be solved using multiplication.
ex: Carl can type 8 pages for every 4 pages that Dan can type. If Dan has typed 12 pages, how many pages has Carl typed?
Since Carl types twice as fast as Dan, he will type twice as many pages as Dan. Therefore, when Dan has typed 12 pages, Carl has typed 24 pages.
Additive Relationships
An additive relationship is when a problem presents a proportion which may be solved using addition.
ex: Allie and Bente type at the same speed. Allie started typing first. When Allie had typed 8 pages, Bente had typed 4 pages. When Bente has typed 10 pages, how many has Allie typed?
Students should reason that since the two people type at the same speed, when Bente has typed an additional 6 pages, Allie should have also typed an additional 6 pages, so she should have typed 8+6, or 14, pages.
Proportion
A proportion is a statement that two given ratios are equal.
ex: 2⁄3 = 4⁄6
Week 12
11/9: 6.4(1) Proportional Reasoning
Comparison Model
The comparison model is a bar model which is useful for visualizing proportional multiplication and division.
ex: 1 unit = 14, 1 whole = 4 * 14 = ?
⎕⎕⎕⎕ 4 * 14 = 56
⎕
14
ex: 1 whole = 48, 1 unit = ?
⎕⎕⎕⎕⎕⎕ 48 48 / 6 = 8
⎕
?
Part-Whole Model
The part-whole model is a bar model which is useful for visualizing proportional addition and subtraction.
ex: 6 red marbles and 5 blue marbles altogether
part part
🟥🟥🟥🟥🟥🟥🟦🟦🟦🟦🟦
^-------------------------------^
whole
Ratio
A ratio is denoted as a/b or a:b, where a and b are rational numbers; a comparison of two quantities.
ex: 1:3 boys to girls in a class
Part-to-whole comparison: 1:4 boys to children
Whole-to-part comparison: 4:1 children to boys
Part-to-part comparison: 1:3 boys to girls
11/7: 6.3(2) Fraction Division
Estimation
The same mental math & estimation strategies used with whole numbers may be applied to rational numbers, as well.
ex: 3 1⁄4 * 7 8⁄9
Rounding: 3 * 8 = 24
Range Strategy: between 3 * 7 = 21 & 4 * 8 = 32
ex: 24 5⁄7 * 4 1⁄8
Compatible Numbers: 24 / 4 = 6 or 25 / 5 = 5
Equal Denominators Algorithm
The equal denominators algorithm is an alternate algorithm for division of rational numbers, which is done by first dividing fractions that have equal denominators.
ex: 2⁄3 / 4⁄7 = 14⁄21 / 12⁄21 = 14⁄12
Invert-&-Multiply Algorithm
The invert-&-multiply algorithm means to use the reciprocal of a given rational number and multiply, when asked to divide by a rational number.
ex: 2⁄3 / 5⁄7 = 7⁄5 * 2⁄3 = 2⁄3 * 7⁄5
Division of Rational Numbers
The division of rational numbers can be shown with an area model, on a ruler, or on a number line.
ex: 6 / 3 = 2
1 + 1 + 1 = 3
1⁄2⏀1⁄2 1⁄2⏀1⁄2 1⁄2⏀1⁄2
Week 11
11/2: 6.3 Fraction Multiplication
The Fundamental Law of Fractions is "a/b = (an/bn) if b =/= 0, n =/= 0".
ex: 1⁄2 = (1*3)/(2*3)
Multiplication with Mixed Numbers
Multiplication with mixed numbers can be done by changing them to improper fractions (a) first or using the distributive property (b).
ex. a: 2 1⁄2 * 2 1⁄2 = 5⁄2 * 5⁄2 = 25⁄4
ex. b: 2 1⁄2 * 2 1⁄2 = (2 + 1⁄2)(2 + 1⁄2)
= (2 + 1⁄2) 2 + (2 + 1⁄2) 1⁄2
= 2 * 2 + 1⁄2 * 2 + 2 * 1⁄2 + 1⁄2 * 1⁄2
= 4 + 1 +1 + 1⁄4
= 6 + 1⁄4
= 6 1⁄4
Properties of Multiplication of Rational Numbers
Theorem 6-10 (Multiplicative Property): the rational number 1 is the unique number such that for every rational number a/b, 1 * (a/b) = a/b = (a/b) * 1.
ex: 1 * (1⁄2) = 1⁄2 = (1⁄2) * 1
Theorem 6-11 (Distributive Property): let a/b, c/d, and e/f be any rational numbers, then (a/b)(c/d + e/f) = (a/b) * (c/d) + (a/b) * (e/f) and (a/b)(c/d - e/f) = (a/b) * (c/d) - (a/b) * (e/f).
ex: 1⁄2 * (¼ + ¾) = (1⁄2) * (¼) + (1⁄2) * (¾)
Bar Model for Multiplication of Rational Numbers
The bar model can be used to show the multiplication of rational numbers.
ex: (½) * (⅗) = 3⁄10
⍁⍁⍁⎕⎕
½<⍌⍌⍌⍂⍂
^--^
⅗
Area Model for Multiplication of Rational Numbers
The area model can be used to multiply rational numbers through repeated addition.
ex: 3*(¾) = ¾ + ¾ + ¾ = 9⁄4 = 2 1⁄4
◕ + ◕ + ◕ = ●●◔
10/31: 6.2 Fraction Addition & Subtraction
Estimation with Rational Numbers
Estimation of rational numbers can be done by using benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers.
ex:
59⁄80 -> 60⁄80 = 3⁄4 (high estimate)
31⁄90 -> 30⁄90 = 1⁄3 (low estimate)
Number Line Model for Subtraction of Rational Numbers
The number line model can be used to add rational numbers which have like denominators.
ex: ¾ - ¼ = ½
¾
l------------------->l
¼
l<--------l
<---0---¼---2⁄4---¾---4⁄4--->
Theorem 6-6
Theorem 6-6 (Additive Inverse Property of Rational Numbers): for any rational number a/b, there exists a unique rational number (-a/b), the additive inverse of a/b, such that (a/b) + (-a/b) = 0 = (-a/b) + (a/b).
ex: 1⁄2 + (-1⁄2) = 0 = (-1⁄2) + 1⁄2
Mixed Numbers
A mixed number is the sum of an integer and a proper fraction.
ex: 2 3⁄4
⍁⍁⍁⍁ ⍁⍁⍁⍁ ⍁⍁⍁⎕
Area Model for Addition of Rational Numbers
The area model can be used to add rational numbers which have like denominators.
ex: ⅗ + ⅘ = 7⁄5 = 1 2⁄5
⍁⍁⍁⎕⎕ + ⍁⍁⍁⍁⎕ = ⍁⍁⍁⎕⎕⍁⍁⍁⍁⎕ = ⍁⍁⍁⍁⍁⍁⍁⎕⎕⎕
Number Line Model for Addition of Rational Numbers
The number line model can be used to add rational numbers which have like denominators.
ex: ¼ + ¾ = 4⁄4 = 1
l-------------------->
¼ ¾
l--->l-------------->
<---0---¼---2⁄4---¾---4⁄4--->
Fraction Circle Model for Addition of Rational Numbers
The fraction circle model can be used to add rational numbers which have like denominators.
ex:
◔ ◕ ●
¼ + ¾ = 1
Unit 2
Week 10
10/26: Test
10/24: Review
Week 9
10/19: 6.1(2) Rational Numbers - Fractions
Ordering Rational Numbers
Ordering rational numbers can be accomplished by creating common denominators or numerators or by comparing to a benchmark fraction.
ex: 1/3 = 2/6 because (2/6)/2 = 1/3
Greater than
Greater than for rational numbers with like denominators means that if a, b, and c are integers and b > 0, then a/b > c/d, if, and only if, a > c.
ex: 3/4 > 1/4
Theorem 6-2
Theorem 6-2 (Equality of Fractions): two fractions a/b and c/d, with b =/= 0 and d =/= 0, are equal if, and only if, ad=bc.
ex: 24/36 = 6/9 because 24x9 = 216 = 36x6
Equality of Fractions
Equality of fractions can be proved by three methods:
- Simplify both fractions to simplest form.
- ex: 12/42 = 2/7 and 10/35 = 2/7
- Rewrite both fractions with the least common denominator.
- ex: 12/42 = 60/210 and 10/35 = 60/210
- Rewrite both fractions with a common denominator (not necessarily the least).
- ex: 12/42 = 420/1470 and 10/35 = 420/1470
Simplest Form
A rational number a/b is in simplest form if, and only if, GCD (a, b) = 1, that is, if a and b have no common factor greater than 1.
ex: 2/7
Simplifying Fractions
Simplifying fractions is justified by the fundamental law of fractions.
ex: 610 = 6x10 = 6 6 = 2x3 = 2
210 21x10 21 21 7x3 7
Fundamental Law of Fractions
The fundamental law of fractions states that if a/b is a fraction and n is a non-zero number, then a/b = an/bn.
ex: 7/-15 = -7/15
Equivalent or Equal Fractions
Equivalent fractions are numbers that represent the same point on a number line. Two fractions are equivalent if and only if the rational numbers they represent are equal.
ex: 1/3 and 2/6
10/17: 6.1(1) Rational Numbers - Fractions
Rational Numbers on a Number Line
Rational Numbers on a Number Line
ex:
<---l---l---l---l---l---l---l---l---l---l---l---l---l---l---l---l---l--->
-2 -5 -1 -3 0 3 1 5 2
4 4 4 4
Improper Fraction
An improper fraction is a rational number a/b, where a > = b > 0 and is greater than or equal to 1.
ex: 7/4
Proper Fraction
A proper fraction is a rational number a/b, where 0 < = a < b and is less than 1.
ex: 4/7
Set Model
The set model refers to a part of a given set.
ex: 3/5
⚪️ ⚪️
⚫️
⚫️ ⚫️
The number line model reflects a distance on a number line.
ex: 2/3
l===l===l---l
0 1
Bar Model
The bar model consists of equal-sized parts of a whole.
ex: 1/3
⬛️l⬜️l⬜️
Denominator
The denominator of a fraction refers to the number below the line, showing how large the whole is.
ex: 3 in 2/3
Numerator
The numerator of a fraction refers to the number above the line, showing how many of the parts indicated by the denominator are taken.
ex: 2 in 2/3
Rational Numbers
Rational numbers is defined as Q = {(a/b)|a and b are integers and b =/= 0}.
ex: 1/2
Week 8
10/12: 5.2 Integer Multiplication & Division
Ordering Integers
When ordering integers, a number line can be used as an aid in describing greater than and less than relations for the set of integers.
ex: -5 is less than -3 --> -5 < -3
-3 is greater than -5 --> -3 > -5
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
Number Line Model for Division
The number line model can be used to demonstrate division and relate dividing integers to multiplying integers.
ex: -160/4 = -40
4x = -160
4(-40) = -160
-40 -40 -40 -40
l<------l<------l<-------l<------l
<--------l--------l--------l--------l--------l-------->
-160 -120 -80 -40 0
Pattern Model for Division
The pattern model suggests the following:
- a positive integer divided by a positive integer is positive
- ex: 4/2 = 2
- a negative integer divided by a positive integer is negative
- ex: -4/2 = -2
- a positive integer divided by a negative integer is negative
- ex: 4/(-2) = -2
- a negative integer divided by a negative integer is positive
- ex: -4/(-2) = 2
Chip Model for Division
The chip model can be used to illustrate the division of positive and negative integers.
ex: -15/3 = -5
partition -15 into 3 groups
🔴 🔴 🔴 🔴 🔴
🔴 🔴 🔴 🔴 🔴
🔴 🔴 🔴 🔴 🔴
/ | \
🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴 🔴
🔴 🔴 🔴 🔴 🔴 🔴
ex: -10/(-5) = 2
take out 2 groups of -5
(🔴 🔴 🔴) (🔴 🔴 🔴)
<--(🔴 🔴) (🔴 🔴)-->
Properties of Integer Multiplication
Properties of integer multiplication include:
Closure property of multiplication of integers - ab is a unique integer.
ex: 2x3 = 6
Commutative property of multiplication of integers - ab = ba.
ex: 2x3 = 3x2
Associative property of multiplication of integers - (ab)c = a(bc).
ex: (2x3)4 = 2(3x4)
Identity property of multiplication of integers - 1 is the unique integer such that for all integers a, 1*a = a = a*1.
ex: 1x2 = 2 = 2x1
Distributive properties of multiplication over addition of integers - a(b+c) = ab + ac and (b+c)a = ba + ca.
ex: 2(3+4) = 2x3 + 2x4 and (3+4)2 = 3x2 + 4x2
Distributive property of multiplication over subtraction of integers - for all integers a, b, and c, a(b-c) = ab - ac and (b-c)a = ba - ca.
ex: 2(3-4) = 2x3 - 2x4 and (3-4)2 = 3x2 - 4x2
Zero property of multiplication of integers - 0 is the unique integer such that for all integers a, a*0 = 0 = 0*a.
ex: 3x0 = 0 = 0x3
Pattern Model for Multiplication
The pattern model uses repeated addition to demonstrate multiplication.
ex: -2 + (-2) + (-2) = 3 x (-2) = -6
Number Line Model for Multiplication
The number line model can be used to demonstrate multiplication and has 3 rules:
- Always start at zero, and always face the positive direction.
- If the number is positive, walk forward.
- If the number is negative, walk backward.
ex:
a. 2x3 = 6
2 groups of 3
b. 2(-3) = -6
2 groups of -3
c. -2x3 = -6
3 groups of -2
d. -2(-3) = 6
opposite of 2 groups of 3
a.
🐌 3 🐌 3 🐌
l------->l-------->l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
b.
🐌 -3 🐌 -3 🐌
l<-----------l<----------l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
c.
🐌 -2 🐌 -2 🐌 -2 🐌
l<-------l<-----l<------l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
d.
🐌 -3 🐌 -3 🐌
l<-----------l<----------l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
Chip Model for Multiplication
The chip model can be used to illustrate the multiplication of positive and negative integers.
ex: 3 x (-2) = -6
3 groups of -2
(🔴 🔴)
(🔴 🔴)
(🔴 🔴)
ex: -3 x (-2) = 6
remove 3 groups of -2
🟡 🟡 🟡 🟡 🟡 🟡
[(🔴 🔴)(🔴 🔴)(🔴 🔴)]--->
10/10: Fall Break
Week 7
10/5: 5.1 Integer Addition & Subtraction
Subtraction Using Adding the Opposite Approach
Subtraction using adding the opposite approach means that for all integers a and b, a - b = a + -b.
ex: 10 - 5 = 5 or 10 + (-5) = 5
Number Line Model for Subtraction
The number line model for subtraction has 4 rules:
- Always start at zero, and always face the positive direction.
- If the number is positive, walk forward.
- If the number is negative, walk backward.
- Subtraction is modeled by turning around and facing the negative direction.
ex:
a. 5-3 = 2
b. -3-5 = -8
c. -3-(-5) = 2
d. 3-(-5) = 8
a.
🐢 3 🐢
l<--------l
🐌 5 🐌
l--------------->l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
b.
🐢 5 🐢
l<-------------------l
🐌 -3 🐌
l<----------l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
c.
🐢 -5 🐢
l---------------->l
🐌 -3 🐌
l<----------l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
d.
🐢 -5 🐢
l-------------->l
🐌 3 🐌
l------->l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
Chip Model for Subtraction
The chip model can also be used to model subtraction between positive and negative integers, utilizing zero pairs.
ex: 3-(-2) = 5
🟡 🟡 🟡 = 3
🟡 🟡 🟡 🟡 🟡 = 3
🔴 🔴
🟡 🟡 🟡 🟡 🟡 = 5
(🔴 🔴)--->
Properties of Integer Addition
Properties of integer addition include:
Closure property of addition of integers - a + b is a unique integer.
ex: 1+2 = 3
Commutative property of addition of integers - a + b = b + a.
ex: 1+2 = 2+1
Associative property of addition of integers - (a + b) + c = a + (b + c).
ex: (1+2)+3 = 1+(2+3)
Identity property of addition of integers - 0 is the unique integer such that, for all integers a, 0 + a = a = a + 0.
ex: 0+1 = 1 = 1+0
Additive inverse property of integers - for every integer a, there exists a unique integer -a, the additive inverse of a, such that a + -a = 0 = -a + a.
Number Line Model for Addition
The number line model for addition has 3 rules:
- Always start at zero, and always face the positive direction.
- If the number is positive, walk forward.
- If the number is negative, walk backward.
ex:
a. -3+5 = 2
b. -3+-5 = -8
c. 3+-5 = -2
a.
5 🐌
l---------------->l
🐌 -3 🐌
l<----------l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
b.
🐌 -5
l<-------------------l
🐌 -3 🐌
l<----------l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
c.
🐌 -5
l<---------------l
🐌 3 🐌
l------->l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
Chip Model for Addition
The chip model can be used to model addition between positive and negative integers.
ex: -4+3 = -1
🔴 🔴 🔴 🔴
🟡 🟡 🟡
Other Models
Other models include the charged field model and the temperature cube model.
ex:
+ + +
-- -- -- -- -- = -2 charge
🟥 🟥 🟥
🟦 🟦 🟦 🟦 🟦 = -2 temperature
Number Line Model
The number line model has 3 rules:
- Always start at zero, and always face the positive direction.
- If the number is positive, walk forward.
- If the number is negative, walk backward.
ex:
🐌 4 🐌
l----------->l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
🐌 -6 🐌
l<-----------------------l
<---l----l----l----l---l----l----l---l---l----l---l--l---l--l---l---l--l---l--l---l---l->
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
Chip Model
The chip model consists of yellow chips representing positive integers and red chips representing negative integers.
ex:
🔴 🔴 = -2
🟡
🔴 🔴 🔴 = -2
🟡 🟡
🔴 🔴 🔴 🔴 = -2
🟡 🟡 🟡
🔴 🔴 🔴 🔴 🔴 = -2
Absolute Value
Absolute value is the distance between the point corresponding to an integer and 0.
ex: |4| = 4 and |-4| = 4
Integer
Integers include all counting numbers, their opposites, and 0.
ex: ... -3, -2, -1, 0, 1, 2, 3...
10/3: 4.3 GCF & LCM
The prime factorization method is more efficient in finding the prime factorization of each number, if the prime factorizations are easy to find.
ex:
40 = 2^3 x5
12 = 2^2 x3
LCM (40, 12) = 2^3 x3x5 = 120
The intersection of sets method is performed by listing all non-zero whole number multiples of two numbers, finding all common multiples, and picking the least element in that set.
ex:
M8 = {8, 16, 24, 32, 40, 48, 56, 64, 72...}
M12 = {12, 24, 36, 48, 60, 72, 84, 96, 108...}
LCM (8, 12) = 24
The colored rods method can also be used to determine the LCM of two numbers; LCM is the common length of two rods stacked on top of one another to create one train.
ex:
🟩 <- 3 rod
🟦 <- 4 rod
🟦🟦🟦🟦🟦🟦🟦🟦🟦🟦🟦🟦 <- three 4 rods
🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩🟩 <- four 3 rods
🟧🟧🟧🟧🟧🟧🟧🟧🟧🟧🟥🟥
^ 10 rod ^ 2 rod
Number Line Method
The number line method is used to find the LCM of two numbers.
ex:
4 4 4 4
l------------>l------------->l-------------->l---------------->l
3 3 3 3 3
l-------->l--------->l--------->l----------->l----------->l
<-0--1--2--3--4--5--6--7--8--9--10-11-12-13-14-15-16->
Least Common Multiple
Least common multiple - of two non-zero whole numbers a and b is the least non-zero whole number that is simultaneously a multiple of a and a multiple of b.
ex: LCM (8, 12) = 24
Prime Factorization Method
The prime factorization method is more efficient in finding the prime factorization of each number, even when many divisors are involved.
ex:
180 = 2x2x3x3x5 = (2^2 x3)3x5
168 = 2x2x2x3x7 = (2^2 x3)2x7
GCD (180, 168) = 2^2 x 3 = 12
Intersection of Sets Method
The intersection of sets method is performed by listing the whole number divisors of two numbers, finding all common divisors, and picking the greatest common division.
ex:
D20 = {1, 2, 4, 5, 10, 20}
D32 = {1, 2, 4, 8, 16, 32}
GCD (20, 32) = 4
Colored Rods Method
The colored rods method uses a model of two or more non-zero whole numbers built with colored rods to determine their GCF.
ex:
3 rods
🟥🟥🟥
🟩🟩🟩
^6 rod
4 rods
🟥🟥🟥🟥
🟫🟫🟫🟫
^ 8 rod
Greatest Common Divisor
Greatest common divisor (greatest common factor) - of two whole numbers a and b, not both 0, is the greatest whole number that divides both a and b.
ex: GCD (24, 30) = 6
Week 6
9/28: 4.2 Prime & Composite Numbers
Theorem 4-16
Theorem 4-16: if n is a whole number greater than 1 and n is not divisible by any prime p such that p^2 < = n, then n is prime.
ex: 3^2 = 9
Theorem 4-15
Theorem 4-15: if n is composite, then n has a prime factor p such that p^2 < = n.
ex: 2^2 = 4
Prime and Composite Numbers
Prime means any whole number with exactly two distinct, whole number factors.
ex: 7x1=7
Composite includes any whole number greater than 1 that has a whole number factor other than 1 and itself.
ex: 2x2=4 and 4x1=4
Upside Down Division Prime Factorization
Upside Down Division Prime Factorization
ex:
2|260
2|130
5|65
13|13
1
Theorem 4-12
Theorem 4-12 (Fundamental Theorem of Arithmetic): each composite number can be written as a product of primes in one, and only one, way except for the order of the prime factors in the product.
ex: 260 = 2^2 x5x13
Factor Tree
A factor tree can be used for finding and organizing a prime factorization of a number.
ex:
260
/\
26 10
/\ /\
2 13 2 5
Prime Factorization
Prime factorization refers to a factorization containing only prime numbers.
ex: 260 = 26x10 = (2x13)(2x5) = 2x2x5x13 = 2^2 x5x13
Factorization
Factorization refers to an expression of a whole number as a product of factors.
ex: 18=2x9, 18=3x6, and 18=2x3x3
Number of Whole Number Divisors
Number of Whole Number Divisors
1 2 3 4 5 6 7 8 9
1 2 4 6 16 12 24 36
3 9 8 18 30
5 25 10 20
7 14 28
11 15 32
13 21
17 22
19 26
23 27
29 33
31 34
37 35
ex: 12 has 6 divisors and 7 has 2 divisors
Method Used in Elementary Schools to Determine Factors
A method used in elementary schools to determine factors of whole numbers is to use squares of paper or cubes to represent the number as a rectangle.
ex:
1 🔲🔲🔲🔲🔲🔲🔲🔲🔲🔲🔲🔲
12
2 🔲🔲🔲🔲🔲🔲
🔲🔲🔲🔲🔲🔲
6
🔲🔲🔲🔲
3 🔲🔲🔲🔲
🔲🔲🔲🔲
4
1 🔲🔲🔲🔲🔲🔲🔲
7
9/26: 4.1 Divisibility
Divisibility Tests
Divisibility Tests
2: a whole number is divisible by 2 if, and only if, its units digit is divisible by 2; that is, if and only if, the units digit is even.
ex: 10/2=5
5: a whole number is divisible by 5 if, and only if, its units digit is divisible by 5; that is, if and only if, the units digit is 0 or 5.
ex: 10/5=2
10: a whole number is divisible by 10 if, and only if, its units digit is divisible by 10; that is, if and only if, the units digit is 0.
ex: 100/10=10
4: a whole number is divisible by 4 if, and only if, the last two digits of the number represent a number divisible by 4.
ex: 8/4=2
8: a whole number is divisible by 8 if, and only if, the last three digits of the whole number represent a number divisible by 8.
ex: 16/8=2
3: a whole number is divisible by 3 if, and only if, the sum of its digits is divisible by 3.
ex: 21/3=7
9: a whole number is divisible by 9 if, and only if, the sum of the digits of the whole number is divisible by 9.
ex: 27/9=3
Theorem 4-1
Theorem 4-1: for any whole numbers a and d, if d|a and n is any whole number, then d|na.
ex: 10/5 and 10/2, thus 10/(5*2)
Divisible and Divides
Divisible can be defined as if the remainder is 0 when m is divided by n, then m is divisible by n.
ex: 6/3=2 means that 6 is divisible by 3
Divides means for any whole numbers a and b, where b=/=0, b divides a, if, and only if, there is a unique whole number q such that a=bq.
ex: 6/3=2 and 2x3=6
Examples and Corresponding General Statements
Examples General Statements
12 is divisible by 2. a is divisible by b.
2 is a divisor of 12. b is a divisor of a.
12 is a multiple of 2. a is a multiple of b.
2 is a factor of 12. b is a factor of a.
2 divides 12. b divides a.