Fracción Parcial
To name your story, you have to think about the overall message and what you want your audience to understand from the story. Also, make it relevant and easy to remember.
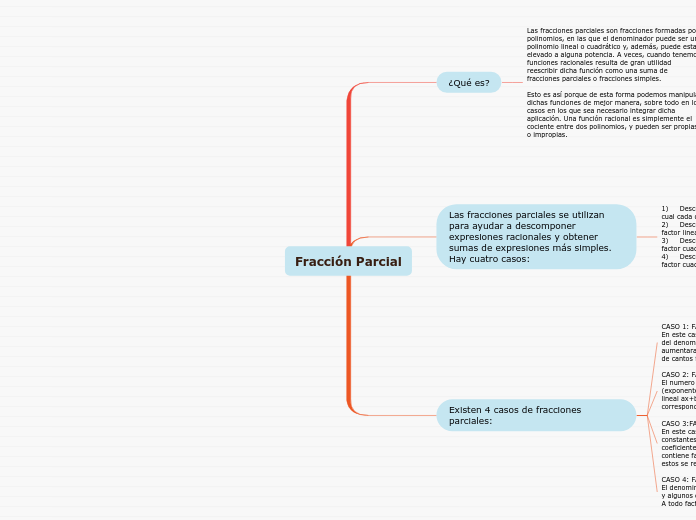
Existen 4 casos de fracciones parciales:
The ending of a story is essential. We all know that if the ending is weak, what happened before loses its importance. So make it unpredictable, but fair. A resolved ending answers all the questions and ties up any loose threads from the plot.
CASO 4: FACTORES CUADRÁTICOS REPETIDOS
El denominador contiene factores de segundo grado y algunos de estos se repiten.
A todo factor de segundo grado repetido n veces.
CASO 3:FACTORES CUADRÁTICOS DISTINTOS
En este caso a cada factor le corresponderán dos constantes, de las cuales una de estas será el coeficiente del termino lineal. El denominador contiene factores de segundo grado, pero ninguno de estos se repite.
CASO 2: FACTORES LINEALES REPETIDOS.
El numero de factores será igual al grado (exponente) del polinomio; es decir; a cada factor lineal ax+b que figure n veces en el denominador le corresponde una suma de fracciones.
This is the closure section of the story.
See examples of possible outcomes below:
- all problems have been solved
- it's clear how each one of your characters ends up
- your main character is transformed by the challenge
CASO 1: FACTORES LINEALES DISTINTOS.
En este caso a cada factor lineal de la forma ax + b del denominador le corresponde una constante, se aumentara en numero de constantes dependiendo de cantos factores se tenga en el denominador.
This is the moment when the main character surpasses the last obstacle and finally faces their greatest challenge.
The climax usually follows one of these patterns:
- realization
- resolution
- choice
Type in your answer.
Las fracciones parciales se utilizan para ayudar a descomponer expresiones racionales y obtener sumas de expresiones más simples.
Hay cuatro casos:
The middle of the story is where you add layers of complications that will lead to the end. Reveal more about the character's journey. Did their personality go through changes? How did they overcome the challenges? And as you build up the story’s central conflict, make it more personal to that character. Also, from the middle act, you have to lead into the final act.
1) Descomposición en fracciones parciales en la cual cada denominador es lineal.
2) Descomposición en fracciones parciales con un factor lineal repetido.
3) Descomposición en fracciones parciales con un factor cuadrático irreducible.
4) Descomposición en fracciones parciales con factor cuadrático repetido.
Each story has a main character and that character usually needs to solve a problem or challenge. The character's challenge is the one that creates tension throughout the story.
Procedimiento para:
Descomposición en fracciones parciales en la cual cada denominador es lineal.
Paso 3:
Si son Descomposición en fracciones parciales en la cual cada denominador es lineal o fracciones parciales con un factor lineal repetido.
Paso 2:
Debo factorizar el denominador para obtener un producto de factores lineales, px +q, o factores cuadráticos irreductibles, y agrupar los factores repetidos para que la función del denominador sea un producto de factores diferentes de la forma, donde o los números m y n no pueden ser negativos.
Paso 1:
Siempre me debo de fijar si el grado de la función del numerador es menor que la del denominador. Si es mayor debo realizar una división larga para bajar el grado de la función del numerador.
¿Qué es?
In the beginning of the story (or the exposition), you will need to introduce the setting and characters. You might also want to introduce the main conflict. This part of the story is important because it gives the reader necessary background information and maybe even a first insight into a character’s personality.
Las fracciones parciales son fracciones formadas por polinomios, en las que el denominador puede ser un polinomio lineal o cuadrático y, además, puede estar elevado a alguna potencia. A veces, cuando tenemos funciones racionales resulta de gran utilidad reescribir dicha función como una suma de fracciones parciales o fracciones simples.
Esto es así porque de esta forma podemos manipular dichas funciones de mejor manera, sobre todo en los casos en los que sea necesario integrar dicha aplicación. Una función racional es simplemente el cociente entre dos polinomios, y pueden ser propias o impropias.
The setting (time & place) of a story can change throughout the plot.
Cuando tenemos una función racional impropia, podemos dividir el polinomio del numerador entre el polinomio del denominador y así rescribir la fracción p(x)/q(x), siguiendo el algoritmo de la división como t(x) + s(x)/q(x), donde t(x) es un polinomio y s(x)/q(x) es una función racional propia.
Una fracción parcial es cualquier función propia de polinomios, cuyo denominador sea de la forma (ax + b)n o (ax2+ bx + c)n, si el polinomio ax2 + bx + c no posee raíces reales y n es un numero natural.
Para poder reescribir una función racional en fracciones parciales, lo primero que se debe hacer es factorizar el denominador q(x) como producto de factores lineales y/o cuadráticos. Uno vez hecho esto se procede a determinar las fracciones parciales, las cuales dependen de la naturaleza de dichos factores.