establece que la suma de las fuerzas externas que actúan sobre un cuerpo y las denominadas fuerzas de inercia forman un sistema de fuerzas en equilibrio
fuerzas generalizadas en el sistema
fuerzas generalizadas en el péndulo doble
el trabajo virtual por variación simultánea de todas las coordenadas
La forma alternativa global, es
para sistemas conservativos
forma general ecuación de Lagrange
Tenemos una ecuación Dinámica.
No aparecen las fuerzas de ligadura
Ecuación simbólica de la dinámica o Principio de D'Alambert
parámetros que determinan la configuración instantánea de un sistema
En los sistemas holónomos, como ya se dijo, la cantidad de coordenadas generalizadas coincide con la cantidad de grados de libertad h del sistema.
Péndulo doble
Barra articulada con cuerpo, sujeto a un resorte deslizante
Cilindro que rueda sobre un plano inclinado.
forma de elipse
ligaduras o vinculos
sistema material capaz de impedir el libre movimiento de partículas
sistema
clasificacion
integridad
holónomas o geométricas
Decimos que un sistema es holónomo, si no tiene vínculos, o bien , si los tiene, éstos son expresables mediante m ecuaciones finitas en los parámetros de Lagrange. Mediante estas m ecuaciones finitas, podemos obtener m parámetros del sistema en función de los otros (n - m) parámetros que hemos tomado como independientes.
no-holónomas
Decimos que un sistema es no holónomo o anholónomo si una, o más, de las m relaciones de vínculo, está expresada como una ecuación diferencial no integrable
dependientes del tiempo
esclerónomas
Se dice que una ligadura es esclerónoma si no depende explícitamente del tiempo. También se les llaman ligaduras fijas o estacionarias
reónomas
Se dice que una ligadura es reónoma si depende explícitamente del tiempo. También se les llaman ligaduras móviles
desigualdades
Bilaterales(o reversibles)
Se da cuando el sistema o cuerpo está permanentemente en contacto con el vínculo, luego se dice que una ligadura es bilateral cuando se expresa mediante una igualdad
Unilaterales
Se dice que una ligadura es unilateral cuando son expresadas mediante una desigualdad.
ecuaciones
Determinación de la posición de un sistema de partículas
Fuerza de ligadura o Reacción de vínculo.
responsables de las restricciones del sistema
cada uno de los desplazamientos virtuales, independientes entre sí, que pueden tener las partículas de un sistema.
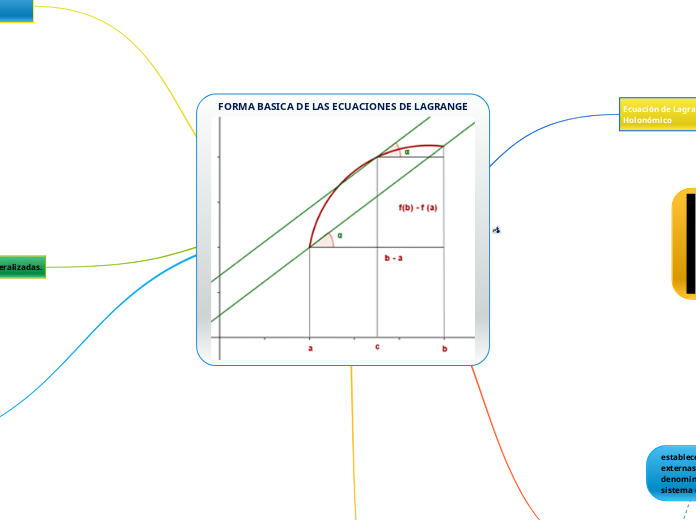
FORMA BASICA DE LAS ECUACIONES DE LAGRANGE
3. Componentes generalizadas de las fuerzas.
Llamaremos trabajo virtual de orden k (o trabajo virtual asociado a la coordenada qk) al trabajo de las fuerzas que actúan en todas las partículas del sistema, cuando las mismas experimentan un desplazamiento virtual parcial de orden k, es decir, un desplazamiento debido a la variación isócrona (o virtual) de una coordenada qk. Indicaremos con  o con
o con  a este trabajo virtual de orden k.
a este trabajo virtual de orden k.
Al referirnos a las fuerzas que actúan en todas las partículas del sistema, incluimos a las fuerzas activas y (al menos en teoría) a las fuerzas de vínculos o ligaduras. Pero como comprobaremos en este artículo, el trabajo de estas últimas siempre resulta nulo y en consecuencia, el trabajo virtual puede calcularse como sólo el trabajo de las fuerzas activas del sistema, excluyendo el trabajo de las fuerzas de ligadura.
Grados de libertad
2. Coordenadas generalizadas.
1. Introducci´on a las ecuaciones de Lagrange
4. Principio de D'Alambert.
tomando como base a
Ecuación de Lagrange para un sistema Holonómico
La ecuación de Lagrange es muy útil para deducir ecuaciones de movimiento usando energías potenciales y cinéticas. Como para calcular esas energías se usan posiciones y velocidades, no se involucra ninguna aceleración y de esta manera la parte cinemática del problema se simplifica mucho. Usando un sistema adecuado de coordenadas adecuado, se pueden obtener las ecuaciones de movimiento de una manera sencilla y directa. A continuación se enlistan tres formas de la ecuación de Lagrange: