Escuela de Berlín
Bibliografía: Ruiz. A. (2003). Historia y filosofía de las matemáticas.
Ana Vargas
Ayelén Bentancur
Romina Olivera
Integrantes
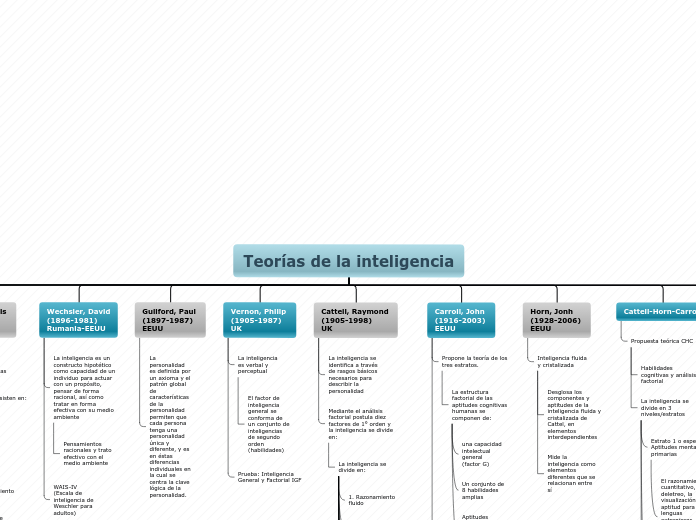
Las Matemáticas en Alemania en el Siglo XIX
En el siglo XIX, las universidades jugaron un rol muy importante en el plano de investigación y ciencia, en donde también en algunas de ellas se crearon laboratorios, siendo a fines del siglo, las universidades más importantes del mundo. Las escuelas técnicas se orientaron en el plano de la ingeniería y minería, y en la técnicas de la producción de textiles
David Hilbert (1862)
Profesor en esa Meca de las matemáticas de la época en Gottingen.
1900: Grundlagen der Geometrie, fue uno de los trabajos de Hilbert con gran influencia, realizó un tratamiento axiomático formal de la geometría clásica, en el utiliza 21 axiomas, en donde usa como objetos definidos los puntos, las rectas y planos, pero 6 relaciones indefinidas: ser congruente, ser paralelo, ser continuo, estar sobre, estar en , estar entere.
1900: Conocido por su intervención en el Congreso Internacional de Matemáticos de París, en donde resumió la trayectoria y las perspectivas de las matemáticas al entrar el siglo XX, en donde formuló 23 proyectos por desarrollar.
Felix Klein (1849)
Sophus Lie(matemático noruego), Klein y Camille Jordan (matemático francés) iniciaron el estudio de la teoría de grupos y los trabajos de Galois.
Klien se centró en la aproximación de grupos discontinuos y Lie en las transformaciones continuas y sus invariantes.
La idea del “Programa de Erlanger” fue considerar que cada geometría era una teoría de los invariantes de un grupo específico de transformaciones, estas se obtenían al ampliar o reducir el grupo.
Otra de las contribuciones de Klien fue que potenció la enseñanza y la investigación de alta calidad en Gottingen, en la tradición de los grandes matemáticos del siglo XIX como Gauss, Dirichlet, y Riemman, y logró convertir esta universidad otra vez en la Meca de las matemáticas occidentales.
1888 y 1893: escribió 3 tomos sobre la teoría de grupos de transformaciones, en especial las cuales corresponden rectas y esferas del espacio euclidiano.
1872: Se convirtió en profesor de la universidad Erlanger, en donde describió la relevancia de los grupos para clasificar especialidades y disciplinas matemáticas.
Gregorg Cantor (1845)
Hubo una disputa entre Kronecker y Cantor en torno a la aceptación del infinito actual, en donde las teorías de Cantor ganaron la aceptación.
1882:Creó un nuevo campo en las matemáticas, teoría de los “agregados” referida a una teoría de cardinales transfinitos (se dio cuenta que no todos los infinitos son del mismo tamaño, y que se podían ordenar)
Richard Dedekind (1831)
1872: contribuyó en la teoría de los números irracionales a través de un concepto llamado "cortadura de Dedekind". En este año publicó un libro donde condensa esta teoría "Stetigkeit ind Irrationale Zahlen
1882: otro libro publicado por Dedekind sobre esta teoría "Was sind und was sollen die Zahle"
Bernhard Riemann (1826)
Realizó su tesis sobre las funciones: u+iv=f(+iy), la cual condujo a las superficies de Riemann.
Presentó dos artículos: uno sobre series trigonométricas y los fundamentos del análisis y otro sobre los fundamentos de la geometría.
Introdujo el concepto de Integral de Riemann
Dio ejemplos de una función continua son derivadas
1859: Presentó un artículo donde analizó la cantidad de números menor que un cierto número, utilizando la teoría de números complejos y la distribución de números primos. El mismo contiene la "hipótesis de Riemann" sobre la función z de Euler.
1857: Encontró una forma de clasificar las funciones abelianas
Leopold Kronecker (1823)
Hizo contribuciones en las funciones elípticas, en la teoría de ideales y en la aritmética de las formas cuadráticas
Defendió por la aritmetización de las matemáticas: decía que las matemáticas debían estar basadas en los números naturales
Rechazó la idea de infinito actual y aceptó la definición de una entidad matemática sólo si ésta podía ser verificada en un número finito de pasos
1886: Pronuncio una frase que se hizo famosa: "Dios hizo los números enteros, todo lo demás es obra humana".
Karl Weierstrass (1815)
Escribió varios artículos sobre integrales hiperelípticas y sobre ecuaciones diferenciales algebraicas
Contribuyó notablemente a fundamentar la teoría de las funciones complejas sobre series de potencias
Una de sus contribuciones: “principio de prolongación analítica”: definiendo una función analítica como una serie de potencias (útil en solución de ecuaciones diferenciales en física matemática)
Aportó gran atención a establecer rigor en la teoría de funciones y en el cálculo de variaciones (nociones de mínimo de una función, derivada, continuidad, etc.)
Descubrió que una función continua sobre un intervalo cerrado sobre el eje real puede expresarse en ese intervalo como una serie de polinomios absoluta y uniformemente convergente
Incluyó funciones de varias variables
1842:Descubrió la convergencia uniforme
Ernst Kummer (1810)
Desarrolló la Geometría diferencial de Congruencias. Introdujo los números ideales en la teoría de dominios racionales algebraicos
1846: Creador de la teoría de ideales: a partir de sus intentos fallidos en buscar una demostración al teorema de Fermat
Johann Dirichlet (1805)
Asociado a Gauss y Jacobi
Considerado “el puente viviente entre matemáticos Alemanes y Franceses”.
Profesor de la Universidad de Breslau y ocupó la cátedra de Gauss en Gottingen.
Ofreció una prueba rigurosa de la convergencia de la serie de Fourier.
Estableció el “principio de Dirichlet” en el cálculo de variaciones.
Fue sucedido en Gottingen por Riemann.
1837: “Series de Dirichlet”, el matemático quería demostrar que la sucesión a, a+b,a+2b,a+3b,..,a+nb,... con a y b primos relativos, es posible encontrar un número infinito de números primos.
Carl Gustav Jacobi (1804)
Fue uno de los grandes matemáticos de la época.
Estudió en Berlín y fue profesor en la Universidad de Konigsberg.
Desarrolló una teoría de funciones elípticas basada en las llamadas “Funciones Theta”, las cuales se construyen por medio de series infinitas.
1929: Fundamenta nova theoriae functionum ellipticarum
1841: De formatione el proprietatibus determinanteinumen
Carl Friedrich Gauss (1777)
Reconocido como el "príncipe de las matemáticas"
Fue quien efectuó una representación de los números complejos a través de los puntos en el plano.
Brindó aportes a la astronomía y física.
Estudió el tema del método de mínimos cuadrados, ya considerado por Legendre y Laplace.
Uno de sus resultados conocidos fue , f(z)=w=x+yi curva cerrada simple.
Otros aportes originales: Geometrías no euclidianas, funciones elípticas (tema trabajado por Legendre, y Euler).
1827: público Disquisitiones generales circa superficies curvas
1825 y 1831 publicó trabajos sobre residuos bicuadrados que daban continuación a sus trabajos en el libro, pero usando la teoría de los números complejos.
1801:(Libro Disquisitiones Arithmeticae): introduce la prueba más rigurosa del teorema fundamental del álgebra.
1795: encontró la ley de reciprocidad cuadrática en la teoría de los números.