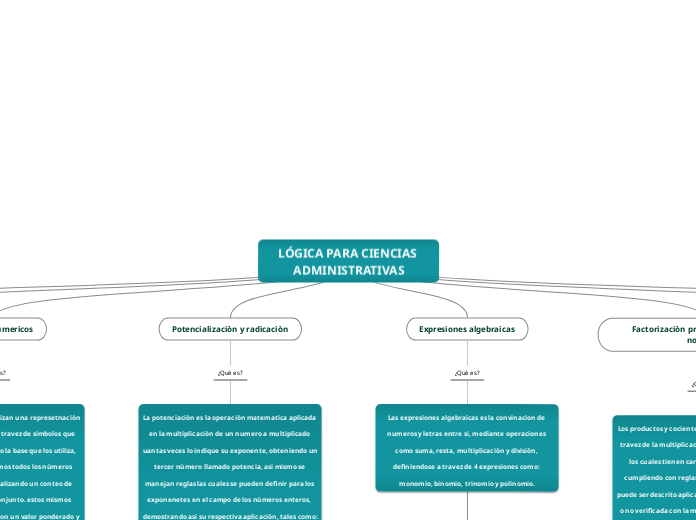
LÓGICA PARA CIENCIAS ADMINISTRATIVAS
Potenciaciòn radicaciòn y logaritmos
Podemos llamarlas tambien como las operaciònes hermanas, sin embargo con algunas diferencias en sus operaciones; com ose habia explicado anterioremnte la potenciacipon es la multiplicacion de un numero n veces, y la radicaciòn lo contrario, por otra parte la logaritmacion nos hace identificar cuantas veces hay que multiplicar B por si mismo para identificar A. Cada una de estas operaciones siempre dara como resultado alguno de estos tres terminos, es decir si quiero identificar la base hago uso de la radicaciòn, si quiero identificar la potencia hago uso de la potenciaciòn, pero si quiero identificar el exponente se usa la logaritmaciòn.
Aplicandola en mi carrera es de suma importancia ya que si se me presenta se que puedo llevara cabo dicho proceso aplicando cada una de sus operaciones las puedo utilizar alguno de estos terminos, ya sea base, esponente o potencia.
Relaciones y funciones
Se expresan a travez de un vinculo entre los elementos de un subconjunto con respecto al producto de dos conjuntos, determinando asi una funciòn matematica del valor de una variable independiente. Tambien e puede llamar como la relaciòn binaria de un conjunto A en un conjunto B.
Se aplica dentro de la carrera profesional a travez de una operaciòn matematica para determinar el valor de una variable depentiente segun el valor de una variable independiente.
Factorizaciòn productos y cocientes notables
Los productos y cocientes notables se llevan a cabo a travez de la multiplicacion de dos o mas polinomios los cuales tienen caracteristicas particulares, cumpliendo con reglas y dando un resultado que puede ser descrito aplicando la multiplicaciòn simple o no verificada con la multiplicaciòn, por otra parte cada producto notable corresponde a una formula de factorizaciòn.
Este mismo es de suma importancia ya que nos ayuda a resolver problemas a travez de reglas generales evitando asi que se hagan muchas operaciones dentro de un desarrollo, siendo mas eficiente en el tiempo.
Expresiones algebraicas
Las expresiones algebraicas es la convinacion de numeros y letras entre si, mediante operaciones como suma, resta, multiplicaciòn y divisiòn, definiendose a travez de 4 expresiones como: monomio, binomio, trinomio y polinomio.
Dentro de mi ambito laboral me sirven para el planteamiento de problemas a travez de nùmeros y letras, de esta forma aplicacido operaciones algebraicas y reduciendo a palabras mas sencillas el plenteamiento de un problema.
Potencializaciòn y radicaciòn
La potenciaciòn es la operaciòn matematica aplicada en la multiplicaciòn de un numero a multiplicado uantas veces lo indique su exponente, obteniendo un tercer nùmero llamado potencia, asi mismo se manejan reglas las cuales se pueden definir para los exponenetes en el campo de los nùmeros enteros, demostrando asi su respectiva aplicaciòn, tales como: (1. multiplicaciòn de potencias de bases iguales, esta explicando que si las bases son iguales sus exponentes se suman; 2. potencia de un producto bajo un exponente dando como resultado la multiplicaciòn de los factores del producto con el mismo exponente; 3. potencia de potencia, aquella que la potencia con exponente dado al ser elevado a otro exponente da como resultado una potencia con los exponentes multiplicados; 4. divisiòn de potencias de bases iguales, en la cual el cociente de potencias con la misma base es igual a la base elevado a la diferencias de llos ecponentes de dichas potencias; 5. potencia de un cociente, es igual al cociente de potencias con el mismo exponente. Por otra parte se entiende la radicaciòn la operaciòn matematica que extrae la raiz de un nùmero, encontrando la base de una potencia a travez de un exponente, de esta forma tambien se puede llamar la operciòn inversa a la potenciaciòn.
La potenciaciòn y radicaciòn nos ayuda a resumir a travez de simbolos operaciones de bases, exponentes y potencias.
Sistemas numericos
Son reglas que permiten realizan una represetnaciòn de los nùmeros naturales, a travez de simbolos que nos ayudan a definirlos como la base que los utiliza, tambien con ellos contruimos todos los nùmeros validos y representarlos, realizando un conteo de elementos que tiene un conjunto. estos mismos estan dentro de un sistema con un valor ponderado y tambien en un sitema posicional compuestos por digitos. Originalemente se vieron desarrollados en el antiguo egipto, a travez de un sitema decimal conocido como el sistema nùmeral Hieratico.
Es de suma importancia dentro de mi carrera ya que a travez de estos representamos todos los nùmeros y trabajar junto con ellos, resolviendo diferentes problemas matematicos que se presenten en la vida, tambien nos sirven para expresar y contar los resultados de una medida y poder realizar diferentes calculos, tambien para codificaciones y tambien en el campo de la fisica para demostrar magnitudes derivadas.
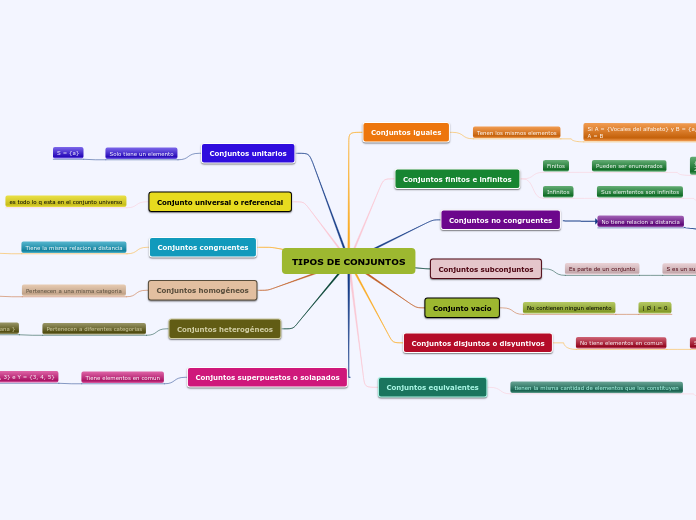
Teoria de conjuntos
Inicialmente estudiada por el matematico Alemàn Georg Cantor siglo XIX, refutada tiempo despues por Zermelo, es la rama de las matematicas, enfocada en los conjuntos, tambien definida como una agrupacion de objetos no repetidos ni ordenados. asi mismo citando a Frege, tenemos que los elementos de un conjunto se pueden definir solo por tal o cual propiedad o tambien citando las palabras de Georfeg Cantor, "un conjunto es la agrupaciòn e un todo de objetos bien diferenciados de nuestra intituciòn o pensamiento"; por otra parte en nuestra actualidad la teoria de conjuntos la efine el sistema ZFC
La teoria de conjuntos como se explico anteriormente como su base principal enfocada en agrupar objetos o elementos segun las necesidades que se presenten, logrando asì procesos mas concretos, simples y rapidos para el desarrollo de actividades contables que compartan ciertas caracteristicas o elementos que nos ayuden a buscar la eficiencia de una actividad.
Introducciòn a la logica
¿Què es?
La logica principalemente se puede referir a una ciencia, la cual se enfoca en buscar la razòn verdadera o falsa de eventos y/o pensamientos; por otra citando algunas palabras del licenciado en Filosofia Fabrizio Pomata en su articulo "Què es la logica y para que nos sirve" podemos entender que la generalidad de la logica entre muchas definiciones ideologicas, la general es que esta misma se encarga de estudiar las leyes del razonamiento valido.
Aplicaciòn en mi carrera
La logica es fundamental dentro de mi carrera como contador publico, hay que entender que dentro de muchos eventos a nivel profesional siempre se debe apoyar por un pensamiento logico, llevando una respuesta ideal para lograr un objetivo propuesto, por otro lado tambien nos sirve para identificar diferentes eventos que se puedan presentar y con la ayuda de esta misma escoger el mas apto y llevar a cabo resultados eficientes dentro del ambito laboral.