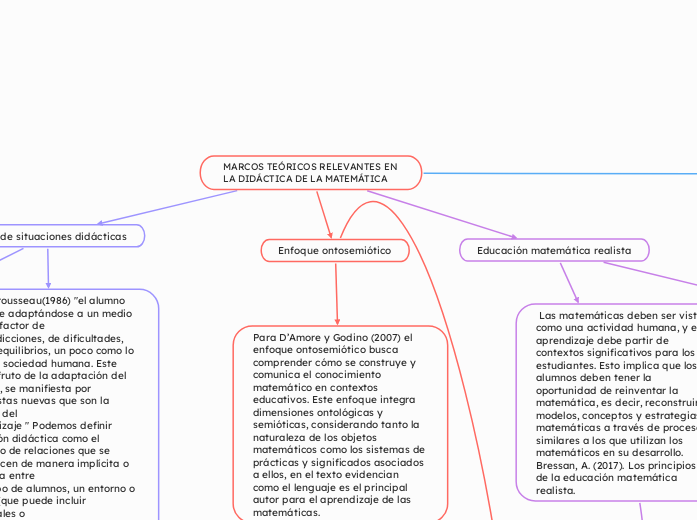
MARCOS TEÓRICOS RELEVANTES EN LA DIDÁCTICA DE LA MATEMÁTICA
Referencias
Bressan, A. (2017). Los principios de la educación matemática realista.
D’Amore y Godino (2007) El enfoque ontosemiótico como un desarrollo de la teoría antropológica en didáctica de la matemática.
Brousseau(1986) Teoría de las situaciones didácticas
Teoría de situaciones didácticas
Se presentaría la división como una herramienta para resolver problemas que implican desafíos y desequilibrios. El aprendizaje surgiría de la necesidad de encontrar soluciones a estas situaciones problemáticas, por ejemplo: Se plantearían problemas de división progresivamente más complejos, donde los estudiantes necesiten adaptar sus estrategias y conocimientos previos para encontrar la respuesta. Por ejemplo, comenzar con repartos iguales sencillos y avanzar a divisiones con residuos, divisiones entre números más grandes, o problemas que requieran interpretar el significado del cociente y el residuo en diferentes contextos.
Permite investigar cómo los individuos aprenden y desarrollan nuevas estrategias en respuesta a desafíos. Es útil para estudiar la dinámica del aprendizaje en entornos complejos y cambiantes. Una de la mayor dificultad es la clasificación de variables a la hora de investigar.
Para Brousseau(1986) "el alumno aprende adaptándose a un medio que es factor de
contradicciones, de dificultades, de desequilibrios, un poco como lo
hace la sociedad humana. Este saber, fruto de la adaptación del
alumno, se manifiesta por respuestas nuevas que son la prueba del
aprendizaje " Podemos definir situación didáctica como el
conjunto de relaciones que se establecen de manera implícita o explícita entre
un grupo de alumnos, un entorno o medio (que puede incluir materiales o
instrumentos) y el profesor, con el fin de que los alumnos aprendan, es decir
que reconstruyan un conocimiento. Brousseau(1986) "Teoría de las situaciones didácticas" (p.2)
Ahora bien, si consideramos el enfoque ontosemiótico, este nos proporciona una lente analítica más profunda sobre la naturaleza de ese aprendizaje. En este sentido, la "situación didáctica" –entendida como el entramado de relaciones entre alumnos, entorno y profesor– constituye el espacio donde los objetos matemáticos adquieren significado. Precisamente, es en este contexto interactivo donde las prácticas y los sistemas de significados asociados a las matemáticas se construyen y se negocian.
Similitudes
Los tres ven el aprendizaje como algo que se construye poco a poco. No es solo memorizar, sino ir armando las piezas para entender algo nuevo.
Los tres ven que el entorno donde aprendemos es importante. Ya sea el desafío del rompecabezas, la conversación con amigos o la situación real de la receta, el "mundo" que rodea al estudiante influye en cómo aprende.
Los tres creen que los estudiantes no son solo "esponjas" que absorben información. Los chicos tienen que estar activos, ya sea pensando mucho, hablando con otros o haciendo cosas prácticas.
Educación matemática realista
Se partiría de contextos significativos y realistas para los estudiantes, donde la división surge de manera natural como una herramienta útil para resolver problemas de su entorno o de situaciones imaginarias pero plausibles, por ejemplo: Se presentarían problemas de división enmarcados en situaciones familiares para los estudiantes (repartir caramelos entre amigos, organizar equipos para un juego, calcular cuántos viajes se necesitan para transportar un grupo de personas)
No se limita a las matemáticas, aplicando al estudio del aprendizaje en ciencias, resolución de problemas en general, e incluso en el desarrollo de habilidades sociales y emocionales. Una gran dificultad que presenta es a la hora de trabajar factores Sociales y culturales, donde puede aparecer un posible descuido.
Las matemáticas deben ser vistas como una actividad humana, y el aprendizaje debe partir de contextos significativos para los estudiantes. Esto implica que los alumnos deben tener la oportunidad de reinventar la matemática, es decir, reconstruir modelos, conceptos y estrategias matemáticas a través de procesos similares a los que utilizan los matemáticos en su desarrollo. Bressan, A. (2017). Los principios de la educación matemática realista.
Además, la propuesta de que los alumnos deben tener la oportunidad de "reinventar la matemática" reconstruyendo modelos, conceptos y estrategias encuentra eco en la forma en que el enfoque ontosemiótico concibe la construcción del conocimiento. Así pues, al enfrentarse a contextos significativos, los estudiantes se involucran en prácticas matemáticas que les permiten dar sentido a los objetos matemáticos, utilizando el lenguaje para comunicar y refinar sus propias construcciones.
Diferencias
Una idea nos dice que debemos dar desafíos interesantes. Otra que debemos hablar con ayuda de un lenguaje técnico y simbólico. La última que debemos usar problemas de la vida real y dejar que los chicos exploren y descubran.
Una idea ve el conocimiento como la habilidad para resolver problemas. Otra lo ve como entender un nuevo "idioma" de símbolos e ideas. La última lo ve como algo que se construye al explorar el mundo.
Para una idea, el lenguaje es una herramienta para mostrar lo que aprendimos. Para otra, es la clave para entender. Para la última, es importante para hablar con otros, pero lo principal es la experiencia práctica.
Enfoque ontosemiótico
Para D’Amore y Godino (2007) el enfoque ontosemiótico busca comprender cómo se construye y comunica el conocimiento matemático en contextos educativos. Este enfoque integra dimensiones ontológicas y semióticas, considerando tanto la naturaleza de los objetos matemáticos como los sistemas de prácticas y significados asociados a ellos, en el texto evidencian como el lenguaje es el principal autor para el aprendizaje de las matemáticas.
Por consiguiente, el lenguaje emerge como un elemento crucial que articula ambos marcos teóricos. Así pues, tal como subraya el enfoque ontosemiótico, la interacción lingüística dentro de la situación didáctica no solo permite al alumno confrontar las "dificultades" inherentes al aprendizaje, sino que también se convierte en la herramienta principal para la construcción y reconstrucción del conocimiento matemático. En otras palabras, las "respuestas nuevas" que testimonian el aprendizaje no son meras soluciones aisladas, sino que, fundamentalmente, representan nuevas formas de expresar y comprender los objetos matemáticos a través del lenguaje.
Se prestaría especial atención al lenguaje y a los significados asociados a la división. Se analizarían los diferentes significados de la división (partes iguales, cociente, razón, operador inverso de la multiplicación), las representaciones (pictóricas, simbólicas, manipulativas) y las prácticas matemáticas relacionadas, por ejemplo: Se utilizarían materiales manipulativos (bloques, fichas), representaciones pictóricas (dibujos, diagramas) y el lenguaje simbólico (÷, /) para conectar los diferentes modos de expresar la división. Se analizarían las ventajas y limitaciones de cada representación.
Potencialidades y limitaciones
Ofrece una base para diseñar intervenciones educativas que intencionalmente presenten desafíos graduados para promover el aprendizaje profundo y una dificulta es el desafío del aprendizaje cognitivo en cada uno de los estudiantes.