MEDIDAS ESTADISTICAS BIVARIANTES DE REGRESION Y CORRELACION
Firstly, make an inventory of the things you already have in your room.
Secondly, close your eyes and imagine your ideal room. Write down the changes you will make to create the room of your dreams.
Redecorating your room is easy and fun!
Modelo de regresión
Determinístico: que bajo condiciones
ideales, la variable independiente puede ser
por una función matemática de las
variables independientes.
Estandarizada: la pendiente β1 nos indica si
hay relación entre dos variables.
Estadístico: Permite la incorporación de un componente aleatorio en la relación.
What do you want to change in your room?
Coeficiente de determinación R2
Determina el grado de correlación entre las variables el coeficiente de determinación también llamado R cuadrado que refleja la bondad del ajuste de un modelo a la variable.
Coeficiente de regresión
Indica el numero de unidades en que se modifica la variable Y por efecto del cambio de la variable independiente X o viceversa en una unidad de medida.
Nulo
Negativo
Positivo
Puede ser lineal, curvilínea o no lineal
Correlación lineal
Grado de correlación
Alta correlación positiva
Correlación positiva
No hay correlación
Correlación débil
Se da cuanto mas separados estén los puntos de la recta.
Correlación fuerte
Se da cuanto mas cerca estén los puntos de la recta
Tipos de Correlación
Correlación nula
Se da cuando no hay dependencia de ningún tipo entre las variables.
Correlación inversa
Se da cuando al aumentar una de las variables la otra disminuye.
Correlación directa
Se da cuando al aumentar una de las variables la otra aumenta.
Trata de establecer la relación o dependencia que existe entre las dos variables que intervienen en una distribución bidimensional, es decir, la determina si los cambios en una de las variables influyen en los cambios de la otra, en caso de que suceda diremos que las variables están correlacionadas
Problemas con la regresión
Errores no corelacionados
Relacion no lineal
Varianza no homogénea
Regresión lineal simple
Covaríanza de dos variables aleatorias X e Y
El signo de la covarianza nos indica que la
nube de los puntos es creciente o no pero
no dice nada del grado de la relación entre
variables.
Entre dos variables, Sxy, nos indica si la
relación entre dos variables es directa o
inversa
Coeficiente de correlación lineal de Pearson
Which are the things from the wardrobe?
Example: clothes, socks, shoes etc.
Tiene un mismo signo que Sxy.
r es útil para determinar si hay relación
lineal entre dos variables. pero no
servirá para (cuadrática, logarítmica).
Si los puntos tiene una tendencia a
disponerse alineadamente
Modelo de Regresión lineal Simple
Encontramos una función de X muy simple
- lineal , que permita aproximar mediante
-ŷ=b0+ b1X
Y el ŷ ya que es rara vez que coincidan por
muy bueno que sea el modelo de regresión
a la cantidad "-e Y-ŷ" se denomina error
residual.
Análisis de la regresión
Estudia la fuerza de la asociación a través
de una medida de asociación denominada
coeficiente de correlación. Modelo de análisis de regresión
Técnica estadística usada para derivar una
ecuación que relaciona una variable de
criterio con una o más variables de
predicción.
Estudia la relación entre dos variables
Cuantitativas
Which are the things that are placed on the ceiling?
Examples: ceiling lamp, phosphorescent sticky stars etc.
Medidas estadísticas Bivariantes
Regresión múltiple
Correlación
Regresion lineal simple
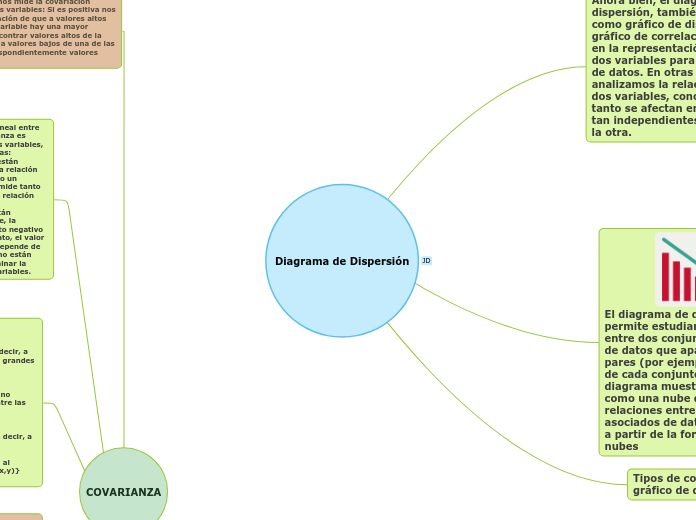
Diagrama de dispersión
Regresión y Correlación
Which are the things that are hanging on the walls?
Examples: paintings, clock, posters, mirrors etc.