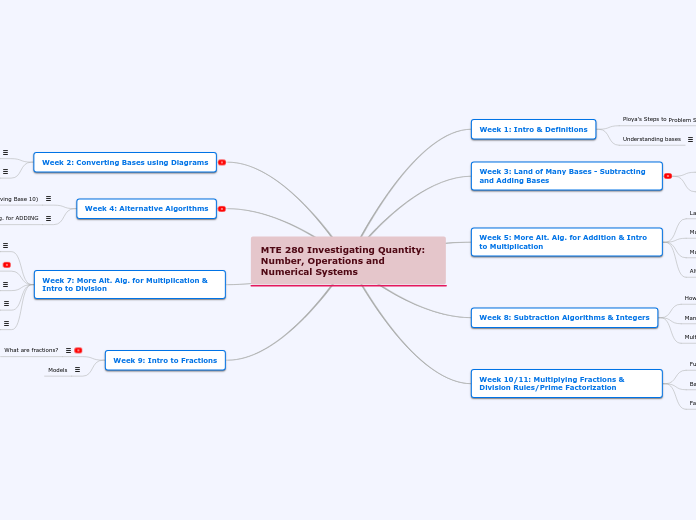
MTE 280 Investigating Quantity: Number, Operations and Numerical Systems
Week 9: Intro to Fractions
Models
Remember: we aren't changing the value, just changing how it looks.
Linear comparison: think length
Set model: group
Area model: 2 shapes
Common denominators are important because when we are adding or subtracting numbers we are adding their areas. In order to add their areas we gave to be talking about the same size pieces.
What are fractions?
Numerators are the number of pieces I have.
Denominators signifies the size of my pieces.
Terminology to utilize: "the numerator is more or less than half way"
Week 7: More Alt. Alg. for Multiplication & Intro to Division
Upwards Division
*ideal method*
This method helps them understand fraction remainders. You have to learn repeated subtraction first because they need to be able to estimate how much of one number goes into another.
Ex:
379/4
How many times does 4 go into 3? 0
How many times does 4 go into 37? 9 with 1 leftover
How many times does 4 go into 19? 4 with 3 left over.
Answer is 94 and 3/4
Traditional Method
"In-n-out" - Use their favorite restaurant to help them remember how to set up division.
You have to teach remainders because of testing, but try to rely more on fractions because that makes more sense.
Repeated Subtraction
The first way to show division.
146 divided by 8. They can ask themselves how many times 8 goes into 146 over and over again. Obviously this is not the most time efficient method, but it works and helps them understand the number on the outside is going into the number on the inside.
Array Method
Teach kids this when you're teaching them the basics of multiplication, like grouping.
Ex:
3(4) = they draw 4 vertical lines intersecting with 3 horizontal lines then count each spot the lines intersect.
Expanded Form
We like this because we're teaching them how to multiply using a form they already know.
Ex:
27(36)
20 + 7
x30 + 6 <--- then you multiply the number on the bottom with each number on top
Week 4: Alternative Algorithms
Alternative Alg. for ADDING
A good algorithm reinforces place value and it is repeatable for many different problems (we don't want a "trick" that only works in a specific scenario).
- Add using expanded form
- 480+364 looks like 400 + 300 + 80 + 60 + 4
- Left to right
- Adding the tens place before the ones place
- Scratch Method
- You make a scratch every time you hit your ten value when adding. Then you add your scratches to see how many tens values you gained. This eliminates the idea of "carry the one". This way kids also don't have to keep a "running total" in their head.
- Trade-off
- Trade around some of the numbers to make the adding easier for you. Only one number here needs to become friendly.
- Friendly #s
- Both numbers need to become friendly numbers. Ex: 28+62 both numbers can be moved around so that they're friendly.
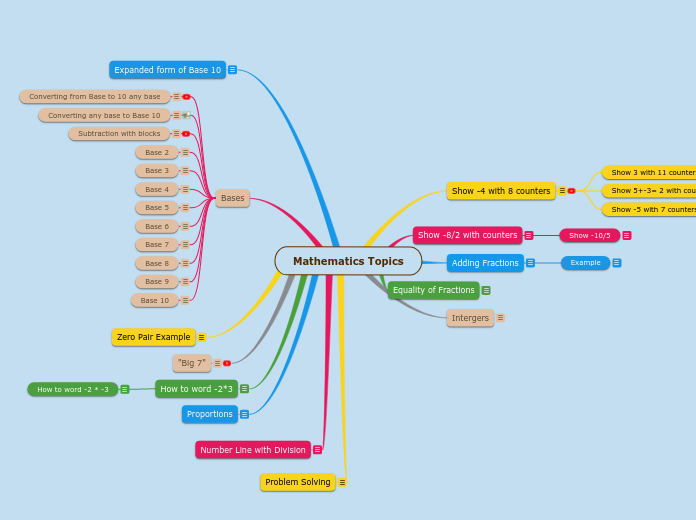
Alternative Algorithms (Leaving Base 10)
Lllleeeaving base ten
When leaving base ten we use upside down division.
Example: 46 to base eight
We ask ourselves how many times 8 goes into 46. Our answer is 5 with a remainder of 6, so the final answer is 56 base eight.
Week 2: Converting Bases using Diagrams
Going from base ten to a different base
Same idea as the previous topic.
In the problem 13 converting to base eight, draw your diagram. This should have 1 long and 3 units. To convert, count your units until you hit eight. This is your new long, so circle eight units. Then add your remaining units. You should end up with 1 long and 5 units. The answer is 15 base eight.
Going from another base to base ten
It's always helpful to draw your diagram.
If given 24 base six, and you want to go to base ten, you can start by drawing 24 base six. That would look like 2 longs and 4 units. Each long here is worth 6 units. Count every single unit in your diagram. 6 + 6 + 4 = 16. The answer is 16 in base ten.
Week 10/11: Multiplying Fractions & Division Rules/Prime Factorization
Factor Trees & Upside down Division
Factor trees: they get to start with the numbers they know. They branch out over and over again and stop when you get to a prime number.
Upside down division: you start by dividing one of their factors that you know to be prime.
LCM: smallest number that is a multiple of both numbers
GCF: Most common factor between two numbers
Backwards C
When we have a mixed number, we use a backwards C to get rid of that mixed number.
Ex:
6 2/5
6x5 + 2 = 32 and then put it over 5
Now you have your improper fraction!
Funky Ones
Funky ones are how we get rid of factors and simplify our fractions. For example, if we have 24/35, we can pull a 6 out of both of those. Then, we can use our funky ones to get rid of the 6.
Week 8: Subtraction Algorithms & Integers
Multiplying Integers & Their Signs
Read it like -5 + 9 = "five negatives plus nine positives".
Different signs being multiplied: negative
Same signs: positive
Manipulatives using Color Counters
Red: always the negative
Other side: always the positive
+ <- we call these together a zero pair
--
This allows us to show a student what zero is.
Ex:
5 + (-4) =
+ + + + +
-- -- -- -- = 1
How do we present it?
The best way to explain subtraction is to take away. That's easiest for the students to visualize. If showing 6 - 2, literally draw 6 units and circle 2, demonstrating you're taking those away. Then they simply count the remainder.
Week 5: More Alt. Alg. for Addition & Intro to Multiplication
Alt. Algorithms for Multiplication
- Base ten blocks method
- 14 x 12, draw the flat, longs, and units. Count what you have
- Area model
- They can multiply like this forever!
- Lattice
- Same as the addition model.
Multiplication Tables
*Post improvement, not success*
What to teach first: 1s, 2s, 10s, 5s
Second: 3s, doubles, 9s
At that point they know most of the table. Then, fill in anything that's left.
Multiplication Meaning
The first number you see is the number of groups.
The second you see is the number of whatever is inside.
2(3) = we have 2 groups of 3 in each
Lattice
In the lattice algorithm you create boxes that help you add together your final answer.
This way is great for kids because they can write the number "12" exactly as they know it. They don't need to worry about carry the one.
Week 3: Land of Many Bases - Subtracting and Adding Bases
Converting Bases w/o Diagrams (SOLVE)
Algorithm for when you're leaving another base and going to base ten
When solving without a diagram, you multiple all of the longs together.
Example:
34 base six converting to base ten:
(6)(6)(6) + (4) = 22
Answer is 22
When we start to see problems with bigger numbers, we do descending exponents.
Example: 231 base four converting to base ten:
2(4^2) + 3(4^1) + 1(4^0) = 45
Adding & Subtracting
When adding, you follow a similar idea as normal adding.
Example: 13 base five + 31 base five
When you add the ones place, you count until you hit five. When you hit five, that becomes a tens place, and vice versa for the tens and hundreds places. Your answer here is 44 base five.
Same idea for subtracting.
Week 1: Intro & Definitions
Understanding bases
Before elementary school, kids need to master 1:1 correspondents (which is assigning value to numbers) and cardinality (which is the ability to see how many numbers there are total).
Examples for understanding bases:
10 < the number 0 shows we have zero extra numbers
^ the number 1 is a ten frame that's been filled
Ploya's Steps to Problem Solving
UnDevCarLo
1) Understand the problem
2) Develop a plan
3) Carry out the plan
4) Look back