jonka angie rojas 5 vuotta sitten
289
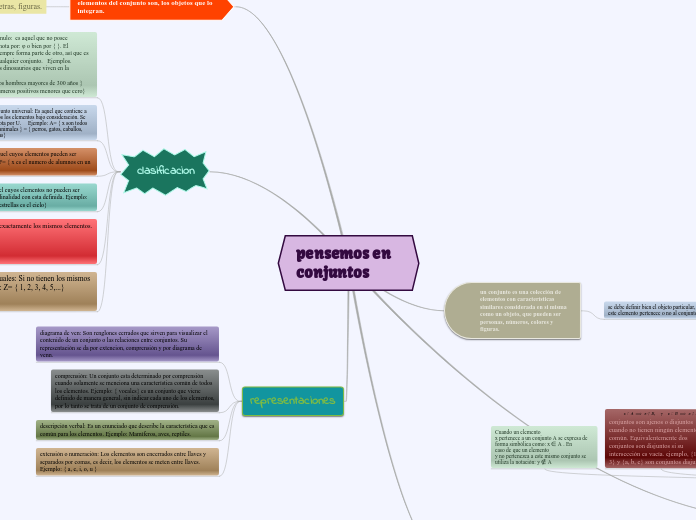
pensemos en conjuntos
La teoría de conjuntos estudia cómo agrupar y relacionar diferentes colecciones de elementos. Una de las operaciones más fundamentales es la unión de conjuntos, donde los elementos de dos o más conjuntos se combinan en uno nuevo.