jonka COSME GABRIEL CUEVA AGUIRRE 2 kuukautta sitten
128
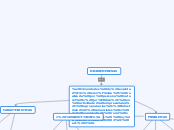
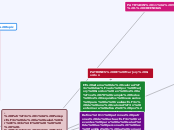
Método simplex de programación lineal, PERT y método CPM.
En la gestión de proyectos, es crucial elegir las herramientas y técnicas adecuadas para asegurar el éxito del proyecto. Dos métodos prominentes son PERT y CPM, ambos utilizando diagramas de red para planificar y coordinar actividades.