REFERENCIA BIBLIOGRAFICA
Trejo Fuentes Saúl. (2008, noviembre 5). Teoría matemática de la administración. Investigación de operaciones. Recuperado de https://www.gestiopolis.com/teoria-matematica-administracion-investigacion-operaciones/
Su énfasis esta en la búsqueda de los medios alternativos. Es un enfoque criticado por preocuparse con el procedimiento y no con el contenido de la decisión.
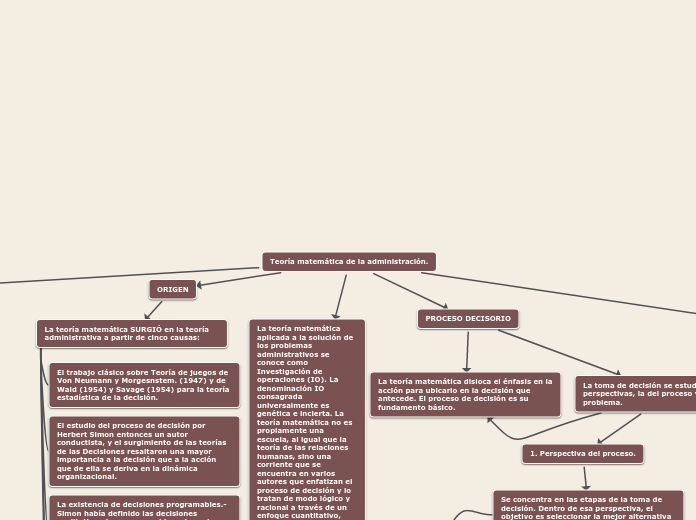
Teoría matemática de la administración.
ESTRATEGIA ORGANIZACIONAL
Aunque la Teoría matemática no se haya caracterizado por incursiones en la estrategia organizacional, ésta se preocupó con la competencia típica de los juegos, donde los elementos básicos de la competencia estratégica son los siguientes
Disposición para actuar.
Capacidad de prever riesgos y utilidades con exactitud y certeza suficientes para justificar la inversión correspondiente.
Recursos que pueden ser permanentemente invertidos en nuevos usos inclusive si los beneficios consecuentes solo aparecieran a largo plazo.
Capacidad de usar esa comprensión para predecir cómo un movimiento estratégico dado alterará el equilibrio competitivo.
apacidad de comprender la conducta competitiva con un sistema en el cual competidores, clientes, dinero, personas y recursos interactúan continuamente.
MODELOS MATEMÁTICOS EN LA ADMINISTRACIÓN
En la teoría matemática, el modelo se utilizaba como simulación de situaciones futuras y evaluaciones de la probabilidad de que suceda.
C.- TIPOS DE DECISIÓN
En función de los problemas estructurados y no estructurados, las técnicas de toma de decisiones (programadas y no programadas)
B.- PROBLEMAS NO ESTRUCTURADOS
El problema no estructurado no puede ser claramente definido pues una o más de sus variables se desconoce o no puede determinarse con algún grado de confianza. El modelo matemático puede tratar a los problemas estructurados y no estructurados con ventajas
Permite respuestas inmediatas y en escala gigantesca por medio de computadoras y equipos electrónicos.
Conduce a una solución segura y cualitativa.
Utiliza técnicas de las matemáticas objetivas y lógicas.
Es susceptible de ampliación por etapas e incluye factores abandonados en las descripciones verbales.
Permite tratar el problema en su conjunto y considerar todas las variables principales simultáneamente.
Descubre relaciones del problema
Permite descubrir una situación mejor
A.- PROBLEMAS ESTRUCTURADOS
Un problema estructurado es aquel que puede ser perfectamente definido pues sus principales variables son conocidas
El problema estructurado puede ser subdividido en tres categorías:
Decisiones bajo incertidumbre.- Las variables son conocidas, pero las probabilidades para evaluar la consecuencia de una acción son desconocidas o no son determinadas con algún grado de certeza.
Decisiones bajo riesgo.- Las variables son conocidas y la relación entre la consecuencia y la acción se conoce en términos probabilísticas.
Decisiones con certeza.- Las variables y sus consecuencias es deterministica.
PROCESO DECISORIO
La toma de decisión se estudia bajo dos perspectivas, la del proceso y la del problema.
2. Perspectiva del Problema
Esta orientado hacia la resolución de problemas.
En loa perspectiva del problema, el que toma la decisión aplica métodos cuantitativos para transformar el proceso de decisión lo mas racional posible concentrándose en la definición y en la elaboración de la ecuación del problema a ser resuelto
1. Perspectiva del proceso.
Se concentra en las etapas de la toma de decisión. Dentro de esa perspectiva, el objetivo es seleccionar la mejor alternativa de decisión. Enfoca el proceso de decisión como una secuencia de tres etapas simples:
Cual es la mejor alternativa de solución (elección)
Cuales son las posibles alternativas de solución al problema.
Definición del problema.
La teoría matemática disloca el énfasis en la acción para ubicarlo en la decisión que antecede. El proceso de decisión es su fundamento básico.
ORIGEN
La teoría matemática SURGIÓ en la teoría administrativa a partir de cinco causas:
La teoría matemática surgió con la utilización de la investigación operacional (IO) en el transcurso de la segunda Guerra Mundial.
La computadora proporciono medios para la aplicación y desarrollo de técnicas de las matemáticas más complejas y sofisticadas.
La existencia de decisiones programables.- Simon había definido las decisiones cualitativas (no programables y tomadas por el hombre) y las decisiones cuantitativas (programables y programadas por el hombre) y las decisiones cualitativas (no programables y programadas para la maquina).
El estudio del proceso de decisión por Herbert Simon entonces un autor conductista, y el surgimiento de las teorías de las Decisiones resaltaron una mayor importancia a la decisión que a la acción que de ella se deriva en la dinámica organizacional.
El trabajo clásico sobre Teoría de juegos de Von Neumann y Morgesnstem. (1947) y de Wald (1954) y Savage (1954) para la teoría estadística de la decisión.
La teoría matemática aplicada a la solución de los problemas administrativos se conoce como Investigación de operaciones (IO). La denominación IO consagrada universalmente es genética e incierta. La teoría matemática no es propiamente una escuela, al igual que la teoría de las relaciones humanas, sino una corriente que se encuentra en varios autores que enfatizan el proceso de decisión y lo tratan de modo lógico y racional a través de un enfoque cuantitativo, detertministico y lógico.