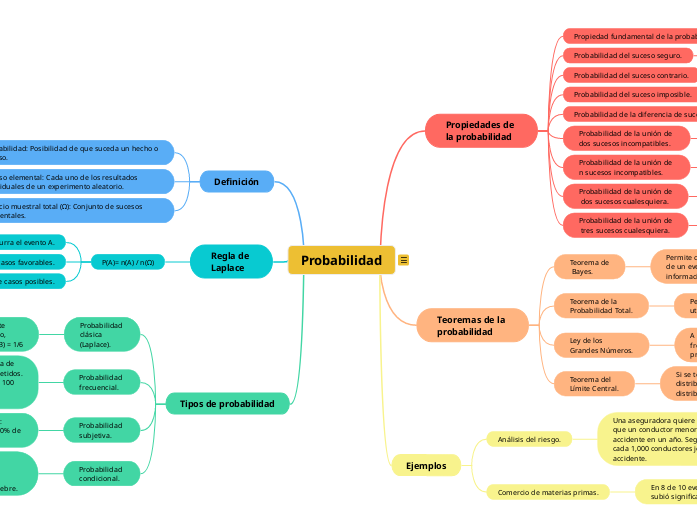
Probabilidad
DEFINICIÓN
La probabilidad es la posibilidad de que suceda un hecho o suceso.
Toda probabilidad tiene: suceso elemental referido a cada resultado de un experimento aleatorio y un espacio muestral total (Ω) compuesto por el conjunto de sucesos elementales.
Regla de LAPLACE
Es la definición clásica de la probabilidad.
P(A) → Probabilidad de que ocurra el evento A.
n(A) → Número de casos favorables.
n(Ω) → Número total de casos posibles en el espacio muestral.
TIPOS DE PROBABILIDAD
Probabilidad Clásica: Se usa cuando todos los resultados son igualmente probables. Ejemplo: Lanzar un dado. La probabilidad de sacar un 3 es P(3) = 1/6.
Probabilidad Frecuencial: Se basa en la frecuencia relativa de un evento en experimentos repetidos. Ejemplo: Al lanzar una moneda 100 veces sale sello 55 veces, la probabilidad estimada es P(sello)= 55/100 = 0.55
Probabilidad Subjetiva: Se basa en el juicio o experiencia personal. Ejemplo: Un meteorólogo estima que hay un 80% de probabilidad de lluvia.
Probabilidad Condicional: Es la probabilidad de que ocurra un evento dado que otro ya ha ocurrido. Ejemplo: La probabilidad de que una persona tenga gripe dado que tiene fiebre.
PROPIEDADES DE LA PROBABILIDAD
Propiedad fundamental de la probabilidad: La probabilidad de un suceso es un número
comprendido entre 0 y 1; es decir: 0 ≤ P(A) ≤ 1 , para todo suceso A .
Probabilidad del suceso seguro: La probabilidad del espacio muestral es 1; es decir: P(Ω) = 1.
Probabilidad del suceso contrario: La probabilidad del suceso contrario de A es: P(A) = 1 − P(A).
Probabilidad del suceso imposible: La probabilidad del suceso imposible es 0; es decir: P(∅) = 0.
Probabilidad de la diferencia de sucesos: Si B está incluido en A entonces: P(A − B) = P(A) − P(B).
Probabilidad de la unión de dos sucesos incompatibles: Si A y B son dos sucesos incompatibles: P(A∪B)=P(A)+P(B)
Probabilidad de la unión de n sucesos incompatibles: P(A1∪A2∪...∪An)=P(A1)+P(A2)+...+P(An)
Probabilidad de la unión de dos sucesos cualesquiera: P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
Probabilidad de la unión de tres sucesos cualesquiera: P(A∪B∪C)=P(A)+P(B)+P(C)−P(A∩B)−P(A∩C)−P(B∩C)+P(A∩B∩C)
TEOREMAS DE LA PROBABILIDAD
Teorema de Bayes: Permite calcular la probabilidad de un evento basándose en información previa.
Teorema de la Probabilidad Total: Sirve para calcular la probabilidad de un suceso específico a partir de información parcial de dicho suceso.
Ley de los Grandes Números: A medida que se repite un experimento, la frecuencia relativa de un evento se acerca a su probabilidad teórica.
Teorema del Límite Central: Si se toman muchas muestras de una población, la distribución de sus medias se aproxima a una distribución normal, sin importar la distribución original de los datos.
EJEMPLOS
Análisis del riesgo
Una aseguradora quiere calcular la probabilidad de que un conductor menor de 25 años tenga un accidente en un año. Si, según datos históricos, de cada 1,000 conductores jóvenes, 150 han tenido un accidente, la probabilidad se calcula como:
Esto significa que hay un 15% de probabilidad de que un conductor joven tenga un accidente.
Comercio de materias primas
Una empresa exportadora de trigo analiza la probabilidad de que el precio del trigo suba debido a fenómenos climáticos extremos, como El Niño. En los últimos 50 años, se registraron 10 eventos de El Niño, en 8 de esos 10 eventos, el precio del trigo subió significativamente.
Si ocurre un fenómeno de El Niño, hay una probabilidad del 80% de que el precio del trigo suba.
Tipos de probabilidad
Probabilidad
condicional.
Probabilidad de que ocurra un evento
dado que otro ya ha ocurrido.
Ejemplo: La probabilidad de que una
persona tenga gripe dado que tiene fiebre.
Probabilidad
subjetiva.
Considera el juicio personal. Ejemplo:
Un meteorólogo estima que hay un 80% de
probabilidad de lluvia.
Probabilidad
frecuencial.
Se basa en la frecuencia relativa de
un evento en experimentos repetidos.
Ejemplo: Al lanzar una moneda 100
veces sale sello 55 veces,
P(sello) = 55/100 = 0.55
Probabilidad
clásica
(Laplace).
Todos los resultados son igualmente
probables. Ejemplo: Lanzar un dado,
la probabilidad de sacar un 3 es P(3) = 1/6
Regla de
Laplace
P(A)= n(A) / n(Ω)
n(Ω) → Número total de casos posibles.
n(A) → Número de casos favorables.
P(A) → Probabilidad de que ocurra el evento A.
Definición
Espacio muestral total (Ω): Conjunto de sucesos elementales.
Suceso elemental: Cada uno de los resultados individuales de un experimento aleatorio.
Probabilidad: Posibilidad de que suceda un hecho o suceso.
Ejemplos
Comercio de materias primas.
En 8 de 10 eventos del Niño, el precio del trigo subió significativamente.
P(A) = 8 / 10
P(A) = 0.8
Hay una probabilidad del 80%
de que el precio del trigo suba.
Análisis del riesgo.
Una aseguradora quiere calcular la probabilidad de que un conductor menor de 25 años tenga un accidente en un año. Según datos históricos, de cada 1,000 conductores jóvenes, 150 han tenido un accidente.
P(A) = 150 / 1,000
P(A) = 0.15
15% de probabilidad de que
un conductor joven tenga
un accidente.
Teoremas de la
probabilidad
Teorema del
Límite Central.
Si se toman muchas muestras de una población, la distribución de sus medias se aproxima a una distribución normal.
Ley de los
Grandes Números.
A medida que se repite un experimento, la frecuencia relativa de un evento se acerca a su probabilidad teórica.
Teorema de la
Probabilidad Total.
Permite calcular la probabilidad de un suceso utilizando probabilidades condicionales.
n
P(B) = Σ P(B|Ai)*P(Ai)
i=1
Teorema de
Bayes.
Permite calcular la probabilidad
de un evento basándose en
información previa.
P(A∣B) = P(B∣A)P(A)
P(B)
Propiedades de
la probabilidad
Probabilidad de la unión de
tres sucesos cualesquiera.
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B)
− P(A ∩ C) − P(B ∩ C) + P(A ∩ B ∩ C)
Probabilidad de la unión de
dos sucesos cualesquiera.
P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
Probabilidad de la unión de
n sucesos incompatibles.
P(A1 ∪ A2 ∪ ... ∪ An) = P(A1) + P(A2) + ... + P(An)
Probabilidad de la unión de
dos sucesos incompatibles.
P(A∪B) = P(A) + P(B)
Probabilidad de la diferencia de sucesos.
P(A − B) = P(A) − P(B)
Probabilidad del suceso imposible.
P(∅) = 0
Probabilidad del suceso contrario.
P(A) = 1 − P(A)
Probabilidad del suceso seguro.
P(Ω) = 1
Propiedad fundamental de la probabilidad.
0 ≤ P(A) ≤ 1