jonka Paul Pozo 4 vuotta sitten
339
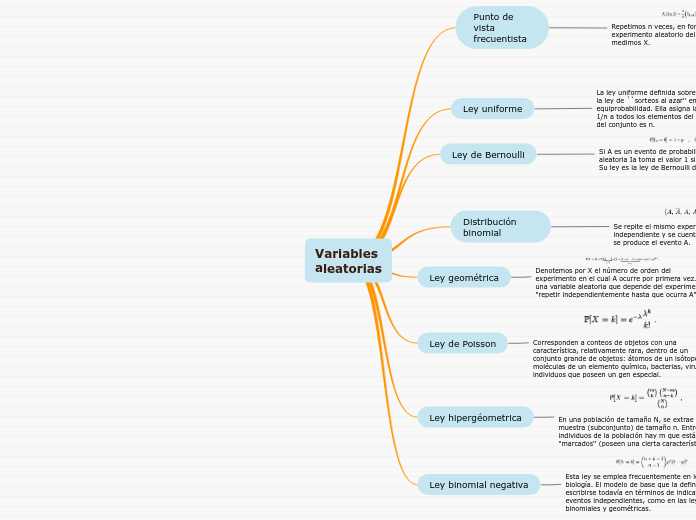
Variablesaleatorias
En el estudio de variables aleatorias y sus distribuciones, se destacan varias leyes que describen diferentes escenarios y propiedades estadísticas. La ley hipergeométrica se aplica cuando se extrae una muestra de una población donde ciertos individuos están marcados por una característica específica.