jonka Francisco Solorio 12 vuotta sitten
261
VM266 8437
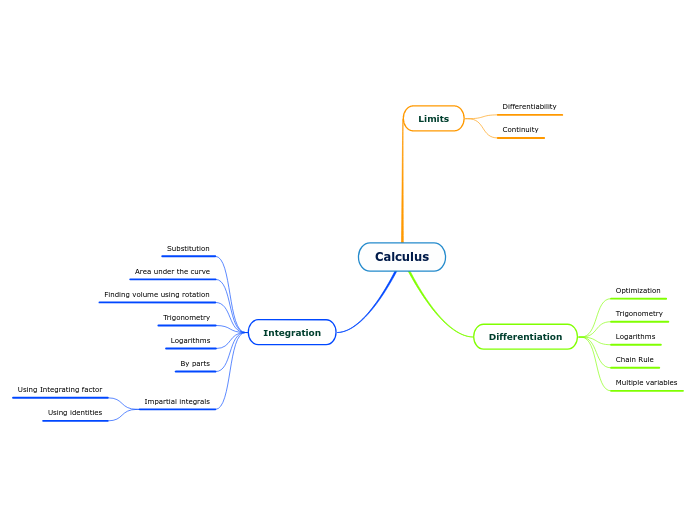
The natural exponential function is a fundamental concept in calculus, involving the mathematical constant e, approximately equal to 2.71828. This function is closely linked with the natural logarithm, denoted as ln, which is the inverse operation of the exponential function.