par camilo ad´res lopez Il y a 3 années
187
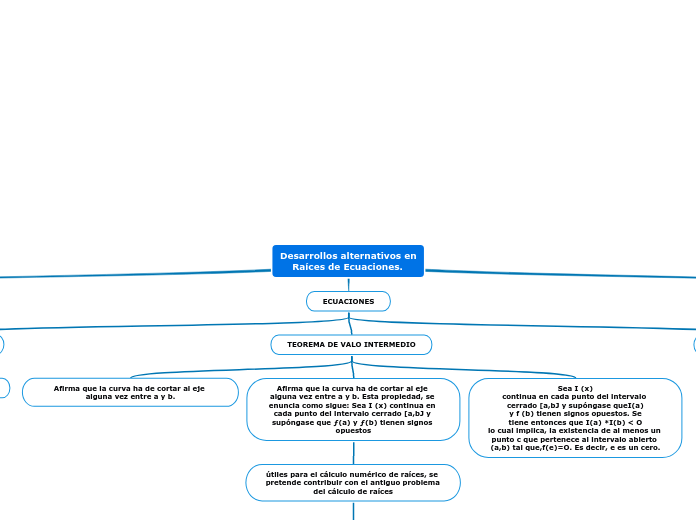
Desarrollos alternativos en Raíces de Ecuaciones.
El texto aborda diversos métodos numéricos para encontrar raíces de ecuaciones, destacando técnicas iterativas y el uso de propiedades matemáticas fundamentales. Se exploran enfoques alternativos que implican la búsqueda aleatoria de soluciones dentro de un intervalo dado.