par Josue Mateo Vicente Il y a 5 années
2124
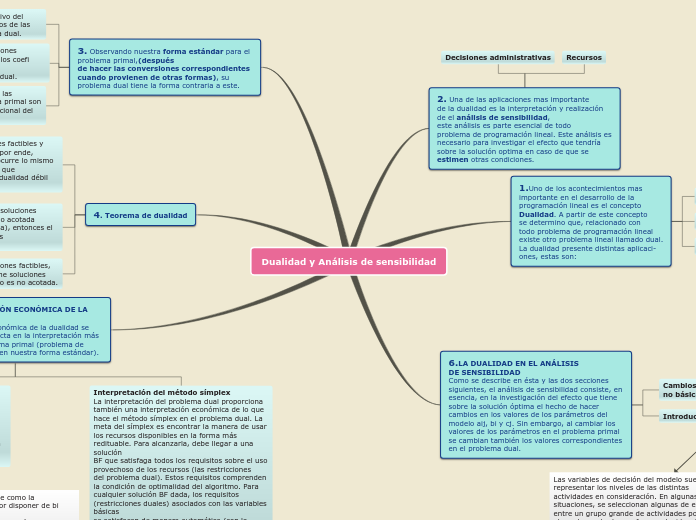
Dualidad y Análisis de sensibilidad
El concepto de dualidad es fundamental en el ámbito de la programación lineal, ya que establece que cada problema lineal tiene un problema dual asociado. Este principio tiene diversas aplicaciones prácticas, entre las cuales destaca el análisis de sensibilidad.