par JAVIER CONTRERAS Il y a 3 années
200
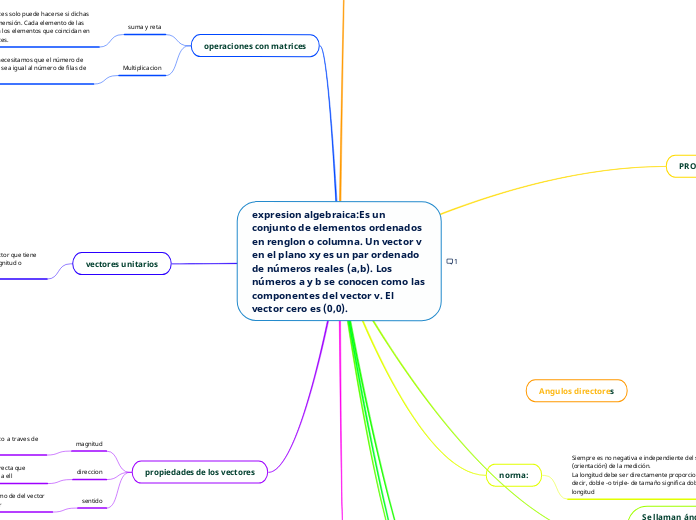
expresion algebraica:Es un conjunto de elementos ordenados en renglon o columna. Un vector v en el plano xy es un par ordenado de números reales (a,b). Los números a y b se conocen como las componentes del vector v. El vector cero es (0,0).
Los vectores en el plano xy son pares ordenados de números reales que se representan como (a, b), donde a y b son las componentes del vector. Un vector unitario o normalizado tiene dirección y sentido, y su magnitud es siempre uno.