par Wilda Auliarahmah Il y a 2 années
996
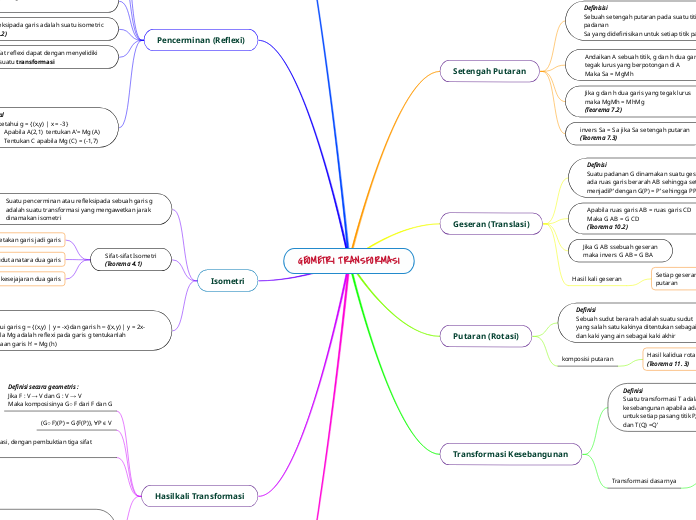
GEOMETRI TRANSFORMASI
Geometri transformasi melibatkan berbagai konsep penting seperti pencerminan, balikan, dan isometri. Transformasi balikan menunjukkan bagaimana setiap transformasi memiliki satu balikan yang unik.