par Fabienne Venant Il y a 5 années
346
HPDIC
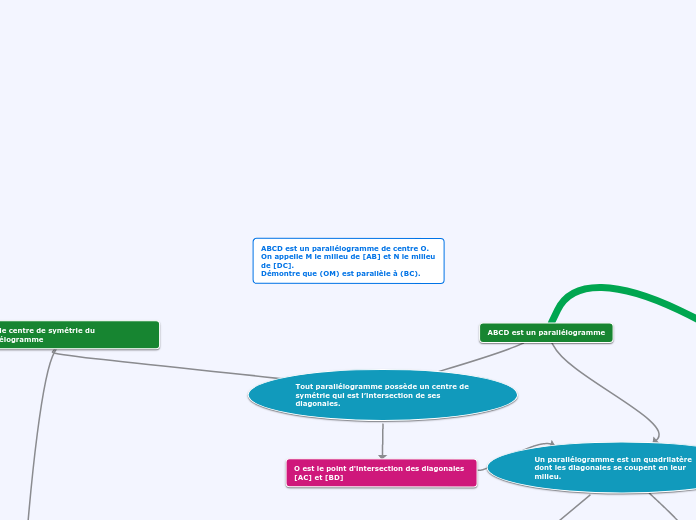
Dans un triangle, une droite passant par les milieux de deux côtés est toujours parallèle au troisième côté. Cette propriété géométrique est souvent utilisée pour démontrer des relations entre les segments et les angles dans diverses figures.