par Angie Ropero Grateron Il y a 2 années
153
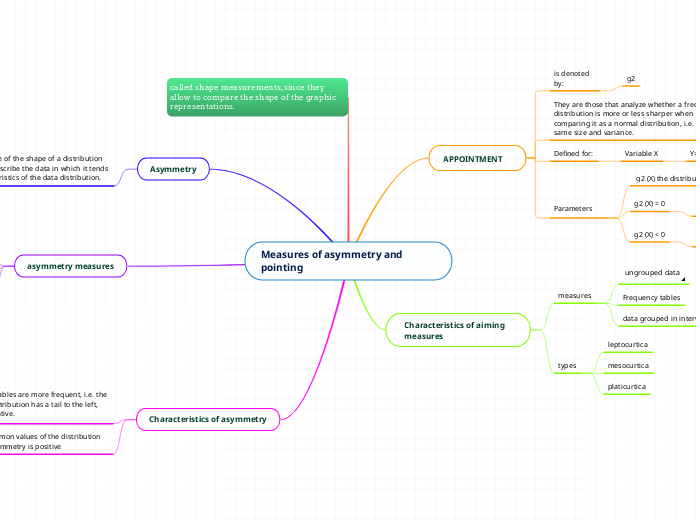
Measures of asymmetry and pointing
The document discusses measures used to analyze the shape of data distributions, focusing on asymmetry and kurtosis. Asymmetry, also known as skewness, assesses how data points are distributed around the mean.