par Joel Arellano Hernández Il y a 3 années
319
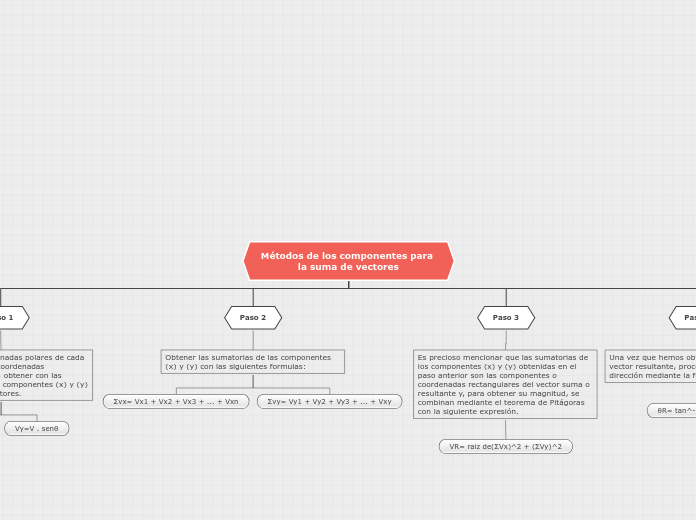
Métodos de los componentes para la suma de vectores
La suma de vectores mediante sus componentes implica varios pasos esenciales. Primero, es necesario convertir las coordenadas polares de cada vector a coordenadas rectangulares, utilizando fórmulas específicas para obtener los componentes en x y y.