par Cristian Mira Il y a 6 années
3831
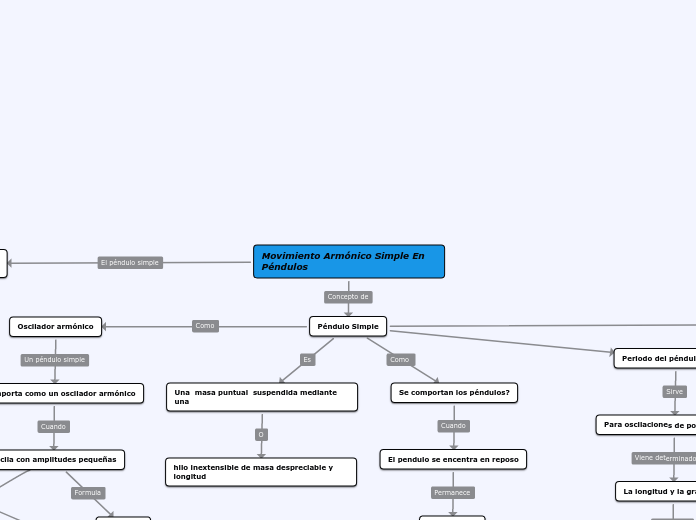
Movimiento Armónico Simple En Péndulos
Un péndulo simple se caracteriza por oscilar con amplitudes pequeñas siguiendo el movimiento armónico simple. Este comportamiento se modela matemáticamente mediante fórmulas que relacionan la aceleración con la distancia a la posición de equilibrio y la longitud del péndulo.