Quadratic Relations

Plus de détails

ODE's

par Taylor Brereton

MAT.105X A7

par David Kedrowski

Eukarya Domain

par RR - 12PC 658658 Lincoln Alexander SS

Grade 3: Parts of a plant

par Umaima Motiwala

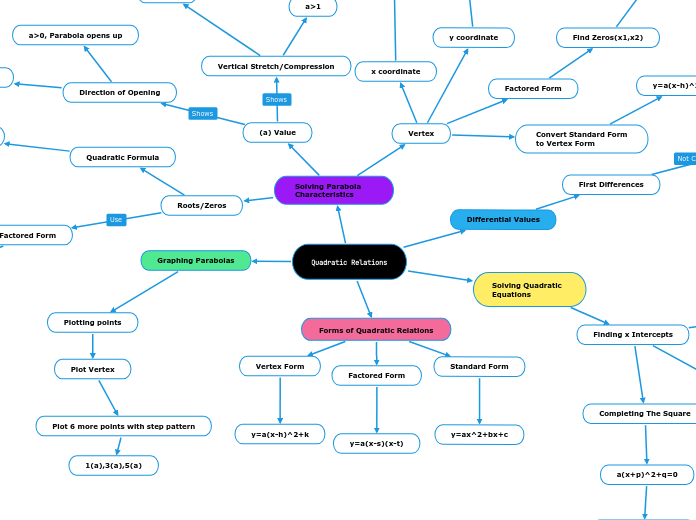
Solving Parabola Characteristics

Vertex

Find Zeros(x1,x2)

Find x coordinate of vertex

(x1+x2) _______ 2

Sub x coordinate of vertex into the equation to find y coordinate of vertex

Convert Standard Form to Vertex Form

(h,k) represent (x,y) of vertex

2(x-2)^2+6 V=(2,6)

y coordinate

Min/Max Value

Max Value

Parabola opens down, max value is the y coordinate of vertex

Min Value

Parabola opens up, min value is the y coordinate of the vertex

x coordinate

Shows axis of symmetry

(a) Value

Direction of Opening

a>0, Parabola opens up

a<0, Parabola opens down

Vertical Stretch/Compression

Vertical Stretch

Vertical Compression

Roots/Zeros

Quadratic Formula

Discriminant Formula

b^2-4ac

Nature of Roots

Discriminant <0

2 Distinct Real Roots

Discriminant =0

1 Real Root

Discriminant >0

No Real Roots

Can Show The Perfect Square

Discriminant is a perfect square so you don't need to use Quadratic Formula

a(x-s)(x-t)=0

Make each factor =0 to solve

2(x-6)(x+8)

x+8=0 x=-8

x-6=0 x=6

Differential Values

First Differences

Second Differences

Solving Quadratic Equations

Finding x Intercepts

Quadratic formula

x=-b±√b^2-4ac ______________ 2a

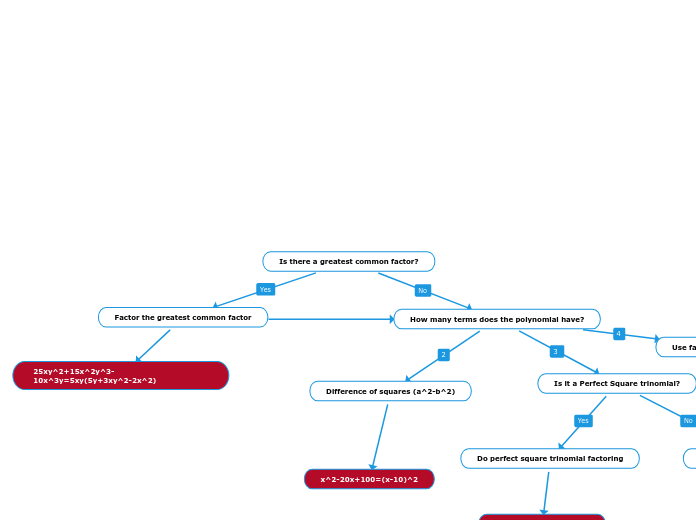
Factoring

Perfect Square Trinomial

Difference of Squares

a2-b2=(a+b)(a-b)

a=1

Simple Trinomial Factoring

x^2+6x+8 (x+4)(x+2)

a>1

Complex Trinomial Factoring

ax^22 + rx + sx + c

Use Grouping and Distributive Property to factor

Completing The Square

a(x+p)^2+q=0

Isolate x for roots

Graphing Parabolas

Plotting points

Plot Vertex

Plot 6 more points with step pattern

1(a),3(a),5(a)

Quadratic Relations