par Vanesa Ibarra Il y a 2 années
140
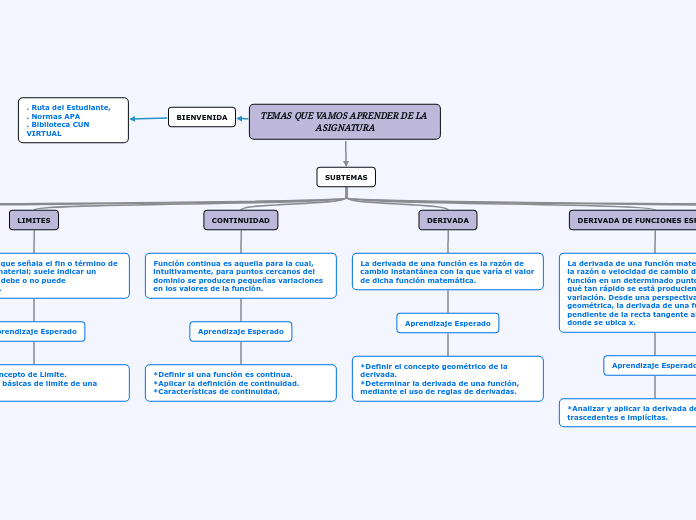
TEMAS QUE VAMOS APRENDER DE LA ASIGNATURA
El curso abarca un conjunto variado de temas fundamentales en matemáticas y habilidades académicas. Se inicia con una guía orientativa para estudiantes, incluyendo la familiarización con las normas APA y el uso de la biblioteca virtual de la institución.