Recuperado de:
-https://www.gestiopolis.com/teoria-matematica-administracion-investigacion-operaciones/
-https://www.monografias.com/trabajos71/teoria-administracion-matematica/teoria-administracion-matematica.shtml
-http://greciaevelin8.blogspot.com/2016/05/teoria-administrativa.html
-https://www.youtube.com/watch?v=4dzrv4BANzQ
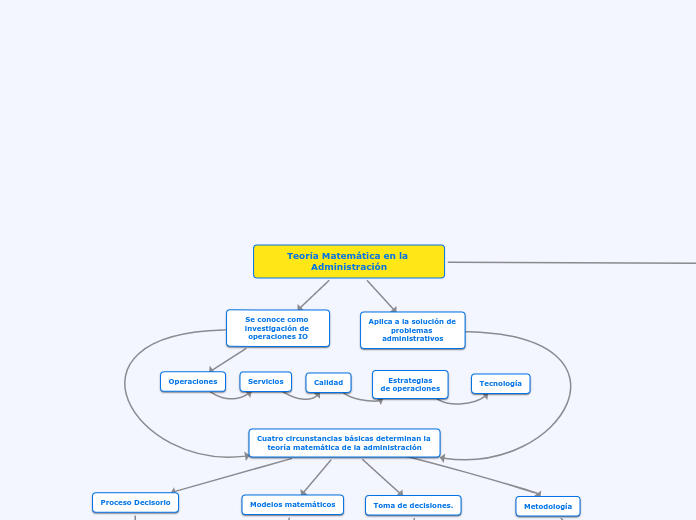
Cuatro circunstancias básicas determinan la teoría matemática de la administración
Metodología
1- Formular el problema
2- Construir un modelo matemático para representarlo
3- Deducir una solución del modelo
4- Probar el modelo y la solución
5- Establecer control sobre la solución
6- Colocar la solución en funcionamiento.
Toma de decisiones.
Con los problemas estructurados y no estructurados, las técnicas para la toma de decisiones se basan en
Uso de técnicas de estadística, probabilidad y modelos matemáticos
Uso del método científico
Visión sistemática de problemas a resolver
Modelos matemáticos
La teoría matemática busca construir modelos matemáticos capaces de simular situaciones reales en las empresas y evaluaciones de la probabilidad que suceda.
Proceso Decisorio
Fundamento básico de la teoría matemática. La toma de decisión se estudia bajo 2 perspectivas
Perspectiva del problema
Perspectiva del proceso
Teoría Matemática en la Administración
Teoría de Juegos
La teoría de juegos nace como una rama de la matemática aplicada que utiliza modelos para la toma de decisiones de 2 o más jugadores. Estudia la toma de decisiones en distintas situaciones.
Sus principales exponentes son: John Von Neuman y John Forbes Nash.
Estrategias
Es el conjunto de movimientos que un jugador toma a lo largo de una partida.
Estrategia óptima:
Es una estrategia que no puede ser superada por otra.
Mixta:
Los movimientos no son los mismos, se deciden por probabilidad.
Estrategia Pura:
Todos los movimientos son los mismos para cualquier situación
Tipos de juegos
Competitivos:
Solo un jugador gana.
Ejemplo:
Monopolio
Cooperativos:
Donde ambos jugadores ganan
Ejemplo:
Rompecabezas
Repetitivos:
Juegos que se repiten con las mismas reglas, pero solo gana uno al final
Ejemplo:
Piedra, papel o tijera.
Suma cero:
Uno gana lo que el otro pierde
Ejemplo:
Poker
Principales características
* 2 Jugadores o más
* Estrategias o decisiones para tomar
*Premios o castigos.
Aplica a la solución de problemas administrativos
Se conoce como investigación de operaciones IO
Operaciones
Servicios
Calidad
Estrategias
de operaciones
Tecnología