a JESSICA RODRIGUEZ 5 éve
1015
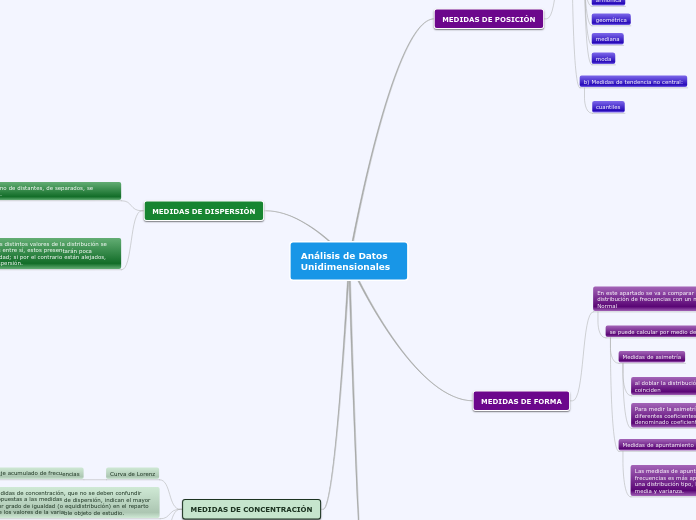
Análisis de Datos Unidimensionales
En el análisis de datos unidimensionales, es fundamental comprender las medidas de dispersión, posición y forma. Las medidas de dispersión evalúan cómo de separados están los datos dentro de una distribución, utilizando métricas como el coeficiente de variación de Pearson, el rango, la varianza y la desviación típica.