APORTES DE NEWTON Y LEIBNIZ EN LA INTEGRAL

Még több ilyen

TEORIAS DE LAS RELACIONES INTERNACIONALES

Szerző: Michelle Comas

IDENTIDAD NACIONAL

Szerző: gloria calderon de la cruz

NUMEROSROMANOS

Szerző: Maria Victoria Correa Argüello

CULTURA PERUANA

Szerző: DANIA LETICIA RUIZ SALINAS

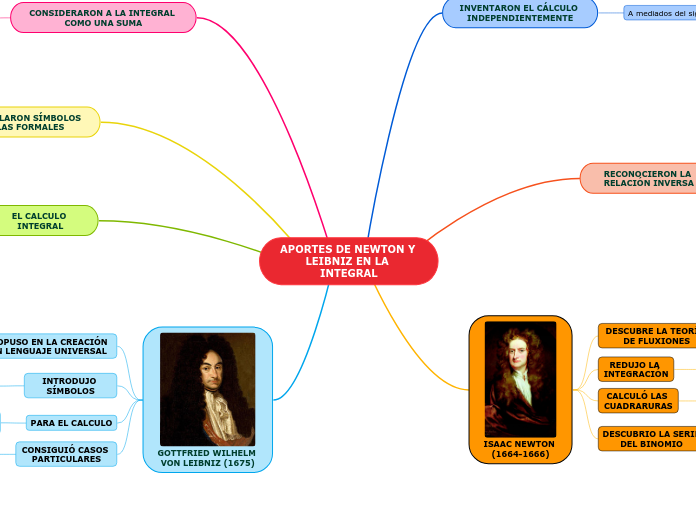
APORTES DE NEWTON Y LEIBNIZ EN LA INTEGRAL

GOTTFRIED WILHELM VON LEIBNIZ (1675)

CONSIGUIÓ CASOS PARTICULARES

De la regla

De la Integración por Partes

PARA EL CALCULO

desarrollo su propia notación

El cual era superior al de Newton

INTRODUJO SÍMBOLOS

para

SE PROPUSO EN LA CREACIÓN DE UN LENGUAJE UNIVERSAL

Para el Álgebra

mediante los símbolos y formulas

que pudieran reducir los cálculos

EL CALCULO INTEGRAL

En aquella época se le conoció como

El Calculo de Cuadraturas

DESARROLLARON SÍMBOLOS Y REGLAS FORMALES

Para su respectivo calculo

CONSIDERARON A LA INTEGRAL COMO UNA SUMA

de infinitos rectángulos infinitesimales

ISAAC NEWTON (1664-1666)

DESCUBRIO LA SERIE DEL BINOMIO

Conocido como

Binomio de Newton

CALCULÓ LAS CUADRARURAS

Calculando su antiderivada

REDUJO LA INTEGRACIÓN

al proceso inverso del calclulo de fluxiones

que se conoce como

el calculo de la primitiva

DESCUBRE LA TEORÍA DE FLUXIONES

el cual proporciono heuristicamente

Algoritmos para el calculo

RECONOCIERON LA RELACIÓN INVERSA

entre

La integración

La derivación

INVENTARON EL CÁLCULO INDEPENDIENTEMENTE

A mediados del siglo XVII

Uniendo y resumiendo en dos conceptos

La Derivada

La Integral