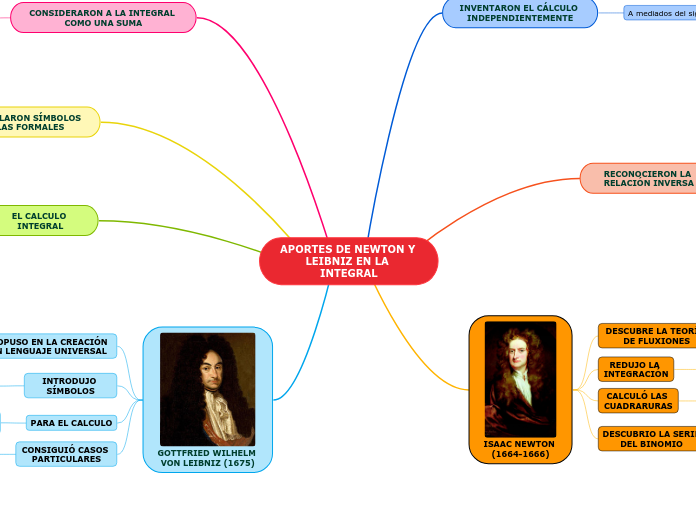
APORTES DE NEWTON Y LEIBNIZ EN LA INTEGRAL
GOTTFRIED WILHELM VON LEIBNIZ (1675)
CONSIGUIÓ CASOS PARTICULARES
De la regla
De la Integración por Partes
PARA EL CALCULO
desarrollo su propia notación
El cual era superior al de Newton
INTRODUJO SÍMBOLOS
para
SE PROPUSO EN LA CREACIÓN DE UN LENGUAJE UNIVERSAL
Para el Álgebra
mediante los símbolos y formulas
que pudieran reducir los cálculos
EL CALCULO INTEGRAL
En aquella época se le conoció como
El Calculo de Cuadraturas
DESARROLLARON SÍMBOLOS Y REGLAS FORMALES
Para su respectivo calculo
CONSIDERARON A LA INTEGRAL COMO UNA SUMA
de infinitos rectángulos infinitesimales
ISAAC NEWTON (1664-1666)
DESCUBRIO LA SERIE DEL BINOMIO
Conocido como
Binomio de Newton
CALCULÓ LAS CUADRARURAS
Calculando su antiderivada
REDUJO LA INTEGRACIÓN
al proceso inverso del calclulo de fluxiones
que se conoce como
el calculo de la primitiva
DESCUBRE LA TEORÍA DE FLUXIONES
el cual proporciono heuristicamente
Algoritmos para el calculo
RECONOCIERON LA RELACIÓN INVERSA
entre
La integración
La derivación
INVENTARON EL CÁLCULO INDEPENDIENTEMENTE
A mediados del siglo XVII
Uniendo y resumiendo en dos conceptos
La Derivada
La Integral