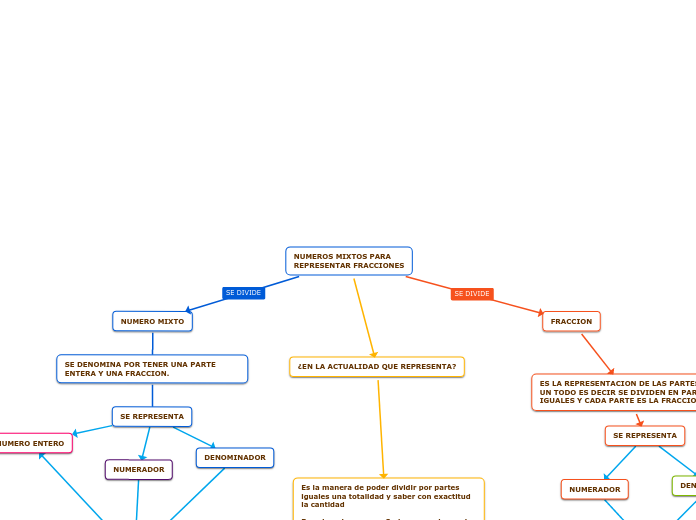
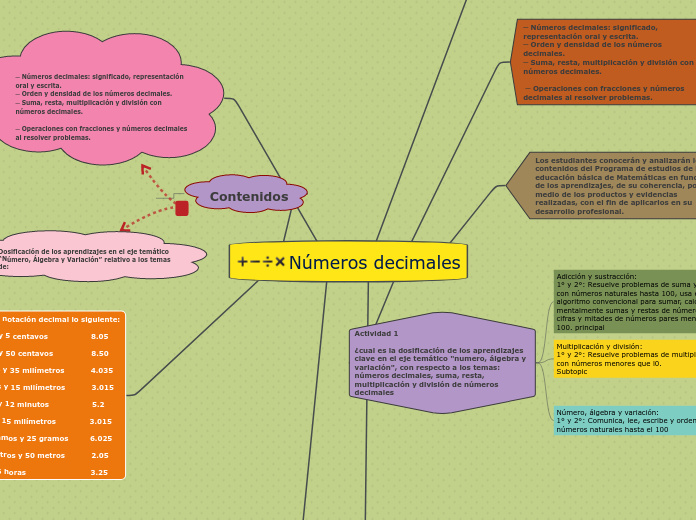
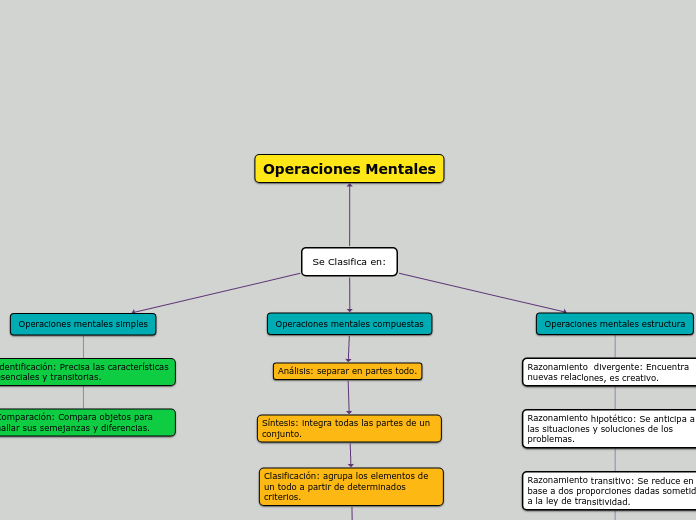
a CLARA CATALINA GARCIA 7 hónapja
86
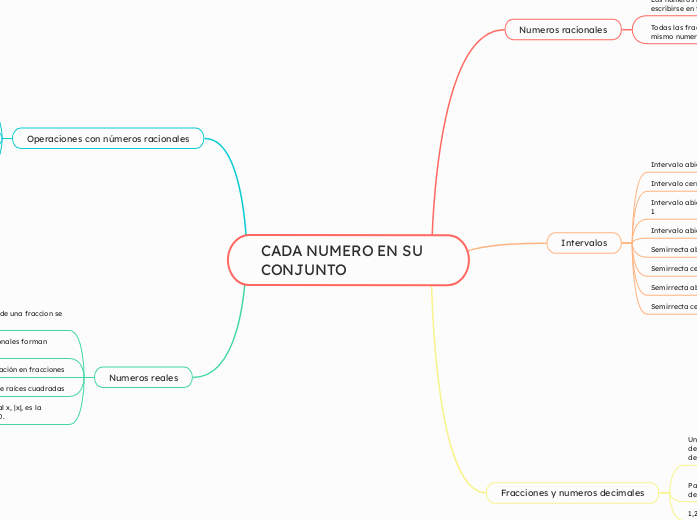
CADA NUMERO EN SU CONJUNTO
En las matemáticas, los números se pueden clasificar y representar de varias maneras dependiendo de sus propiedades. Los intervalos pueden ser abiertos o cerrados, y se utilizan para describir conjuntos de números en una recta numérica.