Calculus - Chapters 3, 4, and 5

Még több ilyen

Chemistry Unit Activities

Szerző: Rebecca Bonham West

First Mind Map

Szerző: J.J. Brunmeier

Fluid Mechanics

Szerző: Tanishq babbar

LASER DIODE

Szerző: saadiah mohamad

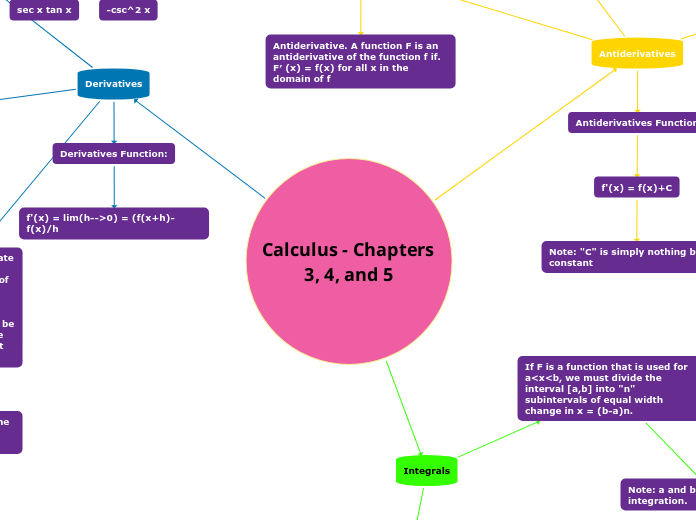
Calculus - Chapters 3, 4, and 5

Integrals

Definite Integral and Indefinite Integral

An indefinite integral is defined as the internal which do not have limits applied to it and it gives a general solution for a problem

∫

Indefinite Integral Properties:

∫ 1 dx = x + C ∫ a dx = ax + C ∫ xn dx = ((xn+1)/(n+1)) + C ; n ≠ 1 ∫ sin x dx = – cos x + C ∫ cos x dx = sin x + C ∫ sec2x dx = tan x + C ∫ cosec2x dx = -cot x + C ∫ sec x tan x dx = sec x + C ∫ cosec x cot x dx = -cosec x + C ∫ (1/x) dx = ln |x| + C ∫ ex dx = ex + C ∫ ax dx = (ax/ln a) + C ; a > 0, a ≠ 1

Function: ∫f(x) dx = F(x) + C

A definite integral is defined as the integral which has upper and lower limits and has a constant value as the solution

Function: ∫ab f(x) dx = F(b)-F(a)

Definite Integral properties:

∫ab f(x) dx = ∫ab f(t) d(t) ∫ab f(x) dx = – ∫ba f(x) dx ∫aa f(x) dx = 0 ∫ab f(x) dx = ∫ac f(x) dx + ∫cb f(x) dx ∫ab f(x) dx = ∫ab f(a + b – x) dx ∫0a f(x) dx = f(a – x) dx

∫ab

If F is a function that is used for a

Note: a and be are the limits of integration.

Antiderivatives

Antiderivatives Function

f'(x) = f(x)+C

Note: "C" is simply nothing but a constant

Let F be an antiderivative of f over an interval I. Then, for each constant C, the function F(x)+C is also an antiderivative of f over I. If G is an antiderivative of f over I, there is a constant C for which G(x)=F(x)+C over I. In other words, the most general form of the antiderivative of f over I is F(x)+C.

It's basically like you're solving a derivatives backwards

A function F is an antiderivative of the function f if. F′ (x) = f(x) for all x in the domain of f

Antiderivative. A function F is an antiderivative of the function f if. F′ (x) = f(x) for all x in the domain of f

Derivatives

Differentiation Rules

Product rule

f′(x) = u′(x) × v(x) + u(x) × v′(x)

Quotient rule

f'(x) = (u'(x)*v(x)-u(x)*v'(x))/(v(x))^2

Chain rule

dy/dx = (dy/du) × (du/dx)

Difference rule

f'(x)=u'(x)-v'(x)

Sum rule

f'(x)=u'(x)+v'(x)

Trig Function

d/dx (cot x)

-csc^2 x

d/dx (sec x)

sec x tan x

d/dx (csc x)

-csc x cot x

d/dx (tan x)

sec^2 x

d/dx (cos x)

-sin x

d/dx (sin x)

cos x

Derivatives Function:

f'(x) = lim(h-->0) = (f(x+h)-f(x)/h

It refers to the instantaneous rate of change of a quantity with respect to the pther. The slope of the tangent line to a curve at a particular point on the curve. Since a curve represents a function, its derivative can also be thought of as the rate of change of the corresponding function at the given point.

When you find the derivative, the value of x gets smaller and smaller.