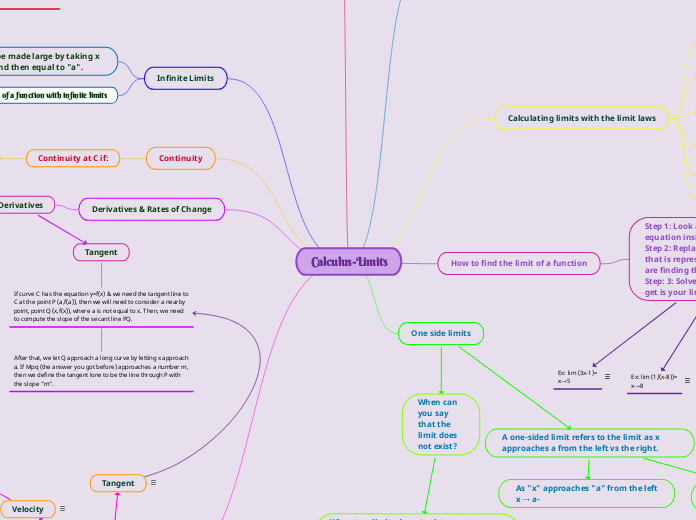
Calculus-Limits

Még több ilyen

Paying Attention to Fractions-002 Group 3

Szerző: Emma Coverdale

Polynomial functions

Szerző: Biftu denko

MAT.126 2.1-2.2

Szerző: David Kedrowski

MAT.126 4.3

Szerző: David Kedrowski

Calculus-Limits

Tangent & Velocity

It is the displacement over time

Instantaneous velocity

The instantaneous velocity is the velocity at a specific time.

Average velocity

The average velocity is the distance travelled over a certain interval of time.

A tangent line is a line that touches a curve at one point.

Derivatives & Rates of Change

Derivatives

Velocity

Tangent

If curve C has the equation y=f(x) & we need the tangent line to C at the point P (a,f(a)), then we will need to consider a nearby point, point Q (x,f(x)), where a is not equal to x. Then, we need to compute the slope of the secant line PQ.

After that, we let Q approach a long curve by letting x approach a. If Mpq (the answer you got before) approaches a number m, then we define the tangent lone to be the line through P with the slope "m".

Derivative - The type of limit that occurs in both tangent lines and velocities.

Continuity

Continuity at C if:

f(a) is defined lim f(x); x->a = f(a) f(x) has a limit as x approaches a

In other words: A function is continuous if a small change in x produces a small change in f(x)

One side limits

A one-sided limit refers to the limit as x approaches a from the left vs the right.

As "x" approaches "a" from the right x → a+

As "x" approaches "a" from the left x → a-

When can you say that the limit does not exist?

When two limits do not exist: When the limit you get when x is approaching a to the left and x is approaching a to the right do not match, the limit when x is approaching a (from both sides) does not exist. DNE

How to find the limit of a function

Step 1: Look at the function and the equation inside of it. Step 2: Replace the "x's" with the number that is representative to "a", since we are are finding the limit as x approaches "a". Step: 3: Solve, then whatever answer you get is your limit.

Ex: lim (x-1)/((x^2)-1)

lim (x-1)/((x^2)-1)

Ex: lim (1/(x-8))= x→8

lim (1/(x-8)) = ∞

x→8

(1/(x-8))

(1/(a-8))

(1/(8-8))

1/0

Ex: lim (3x-1)= x→5

lim (3x-1) = 14

x→5

(3x-1)

(3(a)-1)

(3(5)-1)

(15-1)

14

Calculating limits with the limit laws

The Power Rule

The Constant Rule

lim [cf(x)]; x→a = c·lim f(x); x→a = cL

The Quotient Rule

lim f(x)g(x); x→a = lim f(x); x→a lim g(x); x→a = LM for M≠0

The product Rule

lim (f(x)·g(x)); x→a = lim f(x); x→a · lim g(x); x→a = L·M

The Difference Rule

lim (f(x)−g(x)); x→a = lim f(x); x→a − lim g(x); x→a = L−M

The Sum Rule

lim (f(x)+g(x)); x→a = lim f(x); x→a + lim g(x); x→a = L+M

Formal notation of a function limit

lim f(x) = L x→a

or

lim f(x)=L; x->a

"L" - limit "a" - as "x" approaches (blank)

Infinite Limits

Notation of a function with infinite limits

lim f(x) = ∞ x->a

Values of f(x) can be made large by taking x very close to "a" and then equal to "a".

Limits at infinity

If f(x) doesn't exist as x approaches "a" from the left because the values of f(x) are becoming very large numbers (pos. or neg.) then we say lim x→a− f(x) = ∞ or -∞

If the above behavior happens when x approaches a from the right then we say lim x→a+ f(x) = ∞ or -∞

If both one-sided limits exhibit same behavior then we say lim x→a f(x) = ∞ or -∞

Moreover, in these cases the graph y = f(x) has a vertical asymptote at x = a.

You want to divide the numerator and denominator by the x with the highest exponent in f(x).

This is so that you can get rid of the x's. When you get fractions with x in the denominator, those turn into zero. When you solve, you will find your limit.

Formal notation of a limit at infinity

lim f(x)= L x→∞

Ex: lim √(16x^(2)-8)/(2x-5)=2 x→∞

lim (√(16x^(2)-8))/(2x-5)=2

x→∞

lim (√(16x^(2)-8))/(2x-5) <---Divide the numerator and denominator by x (or multiply by (1/x)).

lim (√(16x^(2)-8)(1/x^2)/(2x-5(1/x^2)) =

x→∞

lim (√(16-(8/x)/(2-(5/x)) =

x→∞

lim (√(16-0))/(2-(0)) =

x→∞

lim (√(16x-0))/(2-(0)) =

x→∞

lim 4/2= 2

x→∞

The limit of f(x) as x approaches infinity is 2.

Ex: lim (1/x)=0 x→∞

lim (1/x) = 0

x→∞

(1/10)=.1

(1/100)=.01

1/1000)=.001

The answer gets smaller and smaller each time, and it gets closer to 0. So, you could say that the limit of (1/x) as x approaches infinity is zero.

lim (1/x) = +∞

x→0+

As you get closer to zero as you come from the right, you get closer to positive infinity.

lim (1/x)m= -∞

x→0-

As you get closer to zero as you come from the left, you get closer to negative infinity.