a YAMILE MUÑOZ 3 éve
483
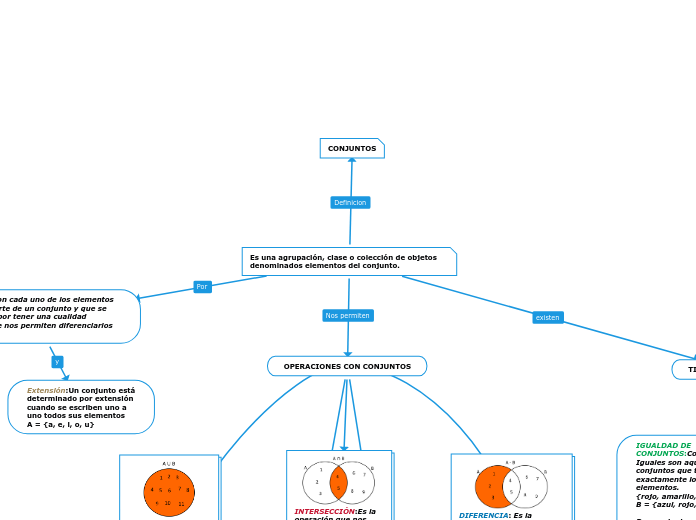
Es una agrupación, clase o colección de objetos denominados elementos del conjunto.
En matemáticas, un conjunto es una colección de objetos llamados elementos, cada uno con una característica única que permite diferenciarlos. Los conjuntos pueden definirse por comprensión, donde se especifica una característica común, o por extensión, donde se enumeran todos los elementos.