a Yolanda Araceli Antonio Cahui 1 éve
94
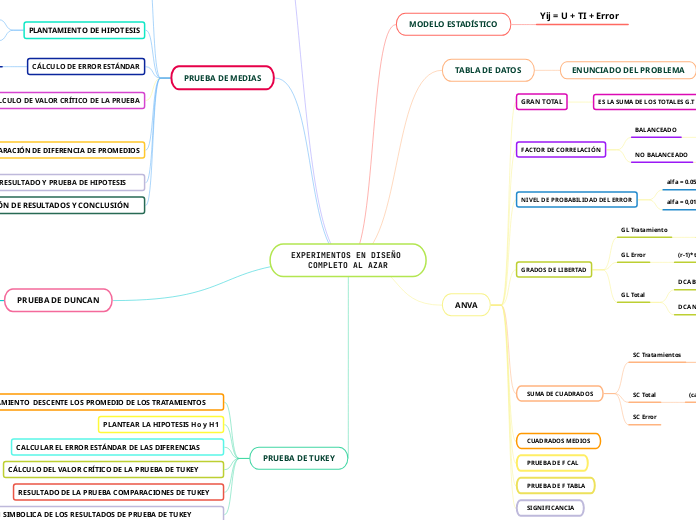
EXPERIMENTOS EN DISEÑO COMPLETO AL AZAR
El texto abarca diferentes aspectos de los experimentos en diseño completamente al azar, enfocados en el uso de la prueba de Duncan para la comparación de medias. Se detalla el procedimiento para plantear hipótesis y decidir si se aceptan o rechazan, utilizando criterios específicos como la diferencia de promedios y el cálculo del valor crítico.