a Catalina Rodriguez 8 éve
831
herramienta web 2.0
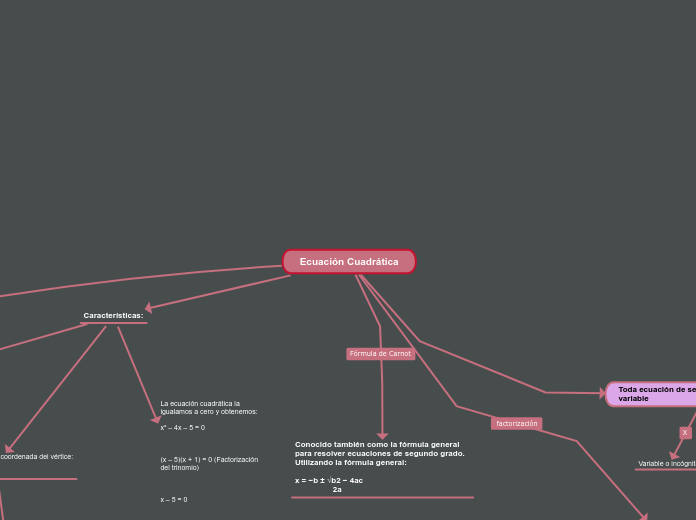
La factorización de trinomios implica encontrar factores comunes y descomponer la expresión en términos más simples. Un trinomio es una expresión algebraica compuesta por tres términos y es común trabajar con trinomios cuadráticos de la forma ax^2 + bx + c.