Productos notables y métodos de factorización

Még több ilyen

Lógicas para ciencias administ

Szerző: LUISA MARIA CASTRO PINEDA

PRODUCTOS NOTABLES

Szerző: FABIO ANDRES RODRIGUEZ RAMIREZ

NÚMEROS REALES(R)

Szerző: Cielo Lora Nieto

PRÉSTAMOS A CORTO PLAZO SIN GARANTÍA

Szerző: Gabyta Narvaez

Productos notables y métodos de factorización

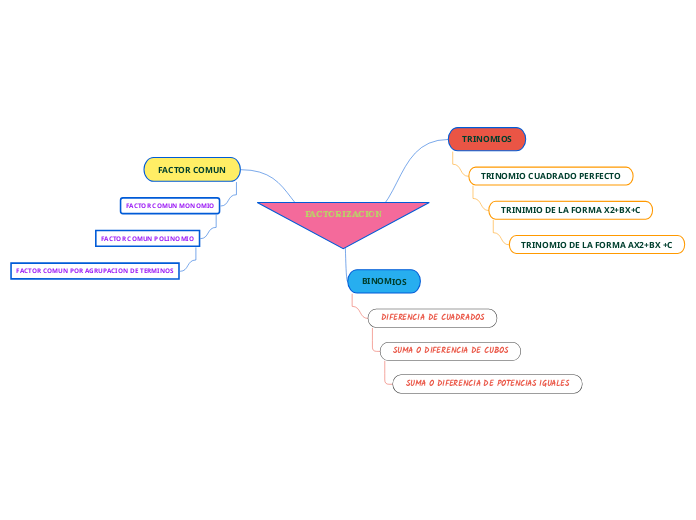
Factorización

Métodos de factorización

Factorización de un trinomio de la forma ax +bx+c

Ordenar el polinomio en forma descendente

Construir una tabla en forma vertical

Donde:

Términos que al multiplicarse den el 1er y 3er término respectivamente para despúes ordenarlos en la factorización.

6y2+7y+2=(3y+2)(2y+1)

Factorización en la forma x2+bx+c

Raíz cuadrada del primer término

Términos que al sumarse o restarse den el 2do término y que al multiplicarse den el 3er término para al final ordenarlos en la factorización.

x2+3x+2=(x+2)(x+1)

Se realizan raíces cuadradas a cada uno de los términos

A partir de una raiz cuadrada en ambos términos por cada binomio se cambia el signo de uno de sus factores.

64x2-36y2=(5x-6y)(5x+6y)

Factorización por suma y resta de cubos

Binomios cuya estructura es a3+b.

Obtener las raíces cúbicas de los términos

Colocar los resultados obtenidos en el primer factor

En el segundo término se coloca la raíz cúbica del primer término al cuadrado

El signo del segundo término al factor debe ser opuestp al segundo término del primer factor.

27m3+64n9=(3m+4n3)(9m2-12mn3+16n6)

Factorización de un trinomio cuadrado perfecto

Trinomio de estructura a2+2ab+b2

Verificar que los términos se encuentren ordenados de acuerdo con los exponentes de mayor a menor.

Hace uso de la raíz cuadrada a través de la cual reduce los términos.

Comprobar el doble producto de las raíces obtenidas.

El resultado es el cuadrado de la suma/resta de las raíces cuadradas de los extremos.

9(a+x)-12(a+x)+4=(3a+3x-2)2

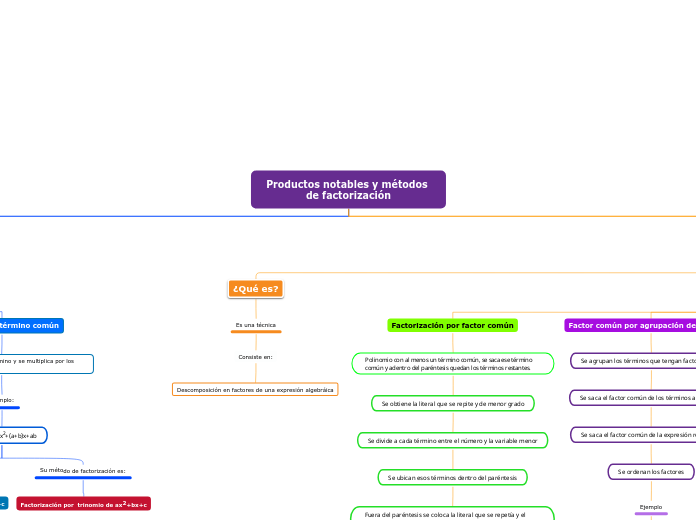
Factor común por agrupación de términos

Se agrupan los términos que tengan factor común.

Se saca el factor común de los términos agrupados

Se saca el factor común de la expresión resultante

Se ordenan los factores

3a-2b-2by4+3ay4=(3a-2b)+(-2by4+3ay4) =1(3a-2b)+y4(-2b+3a)=(3a-2b)(y4+1)

Polinomio con al menos un término común, se saca ese término común y adentro del paréntesis quedan los términos restantes.

Se obtiene la literal que se repite y de menor grado

Se divide a cada término entre el número y la variable menor

Se ubican esos términos dentro del paréntesis

Fuera del paréntesis se coloca la literal que se repetía y el número de meno grado

5x2+2x=x(5x+2)

¿Qué es?

Es una técnica

Consiste en:

Descomposición en factores de una expresión algebráica

Productos notables

Tipos

Binomios con término común

Para resolverlo se toma un término y se multiplica por los otros términos.

(x+a) (x+b)=x2+(a+b)x+ab

Factorización por trinomio de ax2+bx+c

Factorización por trinomio de la forma x2+bx+c

Binomios conjugados

Un binomio tiene signo + y otro binomio con signo -

(a+b) (a-b)=a2-b2

Factorización por diferencia de cuadrados

Binomios al cubo

Consiste en sacarle el cubo a un binomio.

Ejemplo:

(a+-b)3= a3+-3a2b+3ab2+-b3

Factorización por suma o resta de cubos

Cuadrado de un binomio

Se obtiene sumando los cuadrados de sus términos +- el doble producto de los términos en cuestión.

(a+-b)2

Factoriación de un trinomio cuadrado perfecto

Factor común

Se aplica la propiedad distributiva y multiplica a un binomio por un término.

Ejemplo

a · b + a · c = a · (b + c)

Su método de factorización es:

Factorización por agrupación de términos

Factorización por factor común

¿Qué son?

Son multiplicaciones de polinomios.

Con ayuda de ciertas reglas se puede encontrar su resultado.