a Yuri Paola Garcia Bernal 6 éve
244
Sample Mind Map
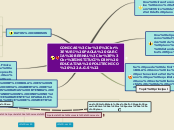
La hipérbola es una curva abierta con dos ramas obtenida al cortar un cono, y se describen mediante varias ecuaciones. Además, se mencionan curiosidades matemáticas como el origen del signo igual, que fue implementado por Robert Recode, y el descubrimiento del cero en India, trasladado a Europa por los árabes.