a LAURA VALENTINA VALIENTE RODRIGUEZ 1 éve
139
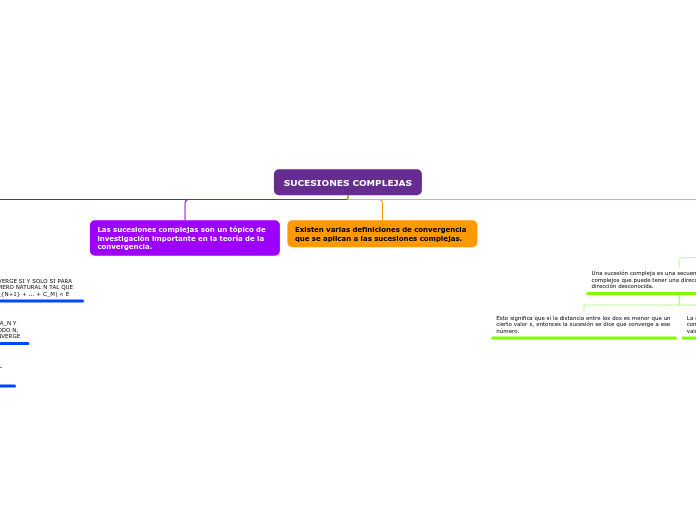
SUCESIONES COMPLEJAS
La investigación sobre sucesiones complejas se centra en la teoría de la convergencia de secuencias de números complejos. Una sucesión compleja puede seguir una dirección específica o desconocida, y su convergencia se determina por la distancia entre la sucesión y el valor de convergencia.