a Javiera Rojo 3 éve
335
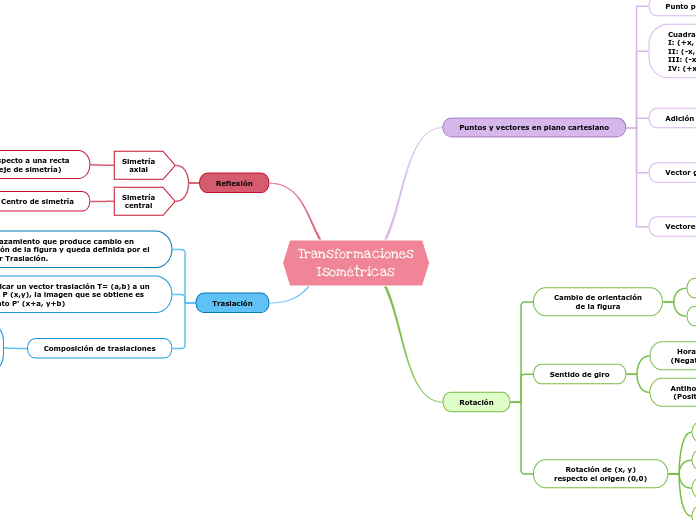
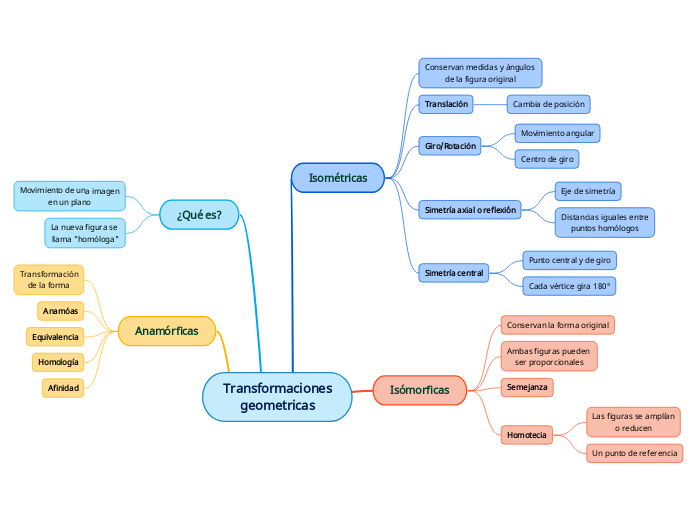
Transformaciones Isométricas
Las transformaciones isométricas son movimientos en el plano que conservan las distancias entre puntos. Estas incluyen rotación, reflexión y traslación. La rotación puede ser en sentido antihorario o horario, alrededor de un punto conocido como centro de rotación, cambiando la orientación de la figura según un ángulo específico.