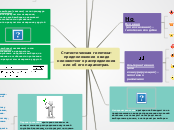
Статический критерий
Наблюдаемое значение критерия – это значение критерия, вычисленное по выборке, то есть зависящее от выборочных значений.
Допустимая область – это область значений критерия, которые не противоречат нулевой гипотезе.
Критические точки – это точки, отделяющие критическую область от допустимой.
Критическая область – это область значений критерия, при которых отвергается нулевая гипотеза и принимается конкурирующая.
Статические гипотезы. Критерии согласия. Параметрические критерии
Виды критериев
Критерии согласия – это критерии, позволяющие оценить степень согласия наблюдаемого статистического распределения выборки с гипотетическим распределением.
Критерий Шапиро – Уилка основан на отношении оптимальной оценки дисперсии к ее обычной оценке. Применение критерия требует специальных таблиц с коэффициентами. Поэтому для числа наблюдений больше 2000, этот критерий неприменим. Критерий Шапиро-Уилка считают лучшим критерием нормальности, так как он обладает большей мощностью перед широким выбором альтернативных критериев нормальности.
Критерий предложен русским математиком Андреем Николаевичем Колмогоровым и применим только для непрерывной случайной величины. Критерий Колмогорова считается наиболее состоятельным для определения степени соответствия эмпирического распределения нормальному, но он мало применим для выборок небольшого объема.
При использовании критериев согласия для проверки согласия с нормальным законом выдвигаются следующие гипотезы:
H1 - функция распределения изучаемой величины не соответствует функции нормального распределения
H0 - функция распределения изучаемой величины соответствует функции нормального распределения
Непараметрические критерии не базируются на предположении о виде распределения изучаемой величины и используют непосредственно выборочные данные, а не параметры выборки.
Параметрические критерии основаны на конкретном виде распределения изучаемой случайной величины (как правило, на нормальном распределении) и используют числовые характеристики выборочной совокупности (выборочную среднюю, выборочную дисперсию и т.п.), которые являются точечными оценками параметров генеральной совокупности.
Проверка гипотез о равенстве генеральных дисперсий двух нормально распределенных генеральных совокупностей. Критерий Фишера -Снедекора.
Гипотезы при использовании критерия Фишера-Снедекора выдвигаются следующим образом:
H0 - генеральные дисперсии равны
H1 - генеральные дисперсии не равны
Если в результате проверки нулевую гипотезу отвергаем, то генеральные дисперсии не равны, выборочные дисперсии различаются значимо.
Если нет оснований отвергать нулевую гипотезу, то генеральные дисперсии равны, выборочные дисперсии различаются не значимо.
Проверка гипотезы о равенстве генеральных средних двух нормально распределенных генеральных совокупностей. Критерий Стьюдента.
Гипотезы при использовании критерия Стьюдента выдвигаются следующим образом:
H0 - генеральные средние равны
H1 - генеральные средние не равны
Применение t-критерия Стьюдента возможно как для зависимых, так и для независимых выборок.
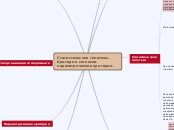
Статистическая гипотеза – это предположение о виде неизвестного распределения или об его параметрах.
В результате проверки статистических гипотез возможны четыре случая:
4) гипотеза Н0 не верна, но не отвергается
Статистическая ошибка II рода.
3) гипотеза Н0 не верна и отвергается
Третий случай означает правильное решение.
2) гипотеза Н0 верна, но отвергается
(Нулевая гипотеза верна, но отвергается) говорят, что совершается статистическая ошибка I рода.
1) гипотеза Н0 верна и не отвергается
Первый случай означает правильное решение.
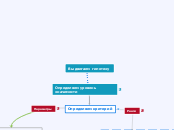
Основной принцип принятия решения при проверке статистических гипотез состоит в следующем: гипотеза отвергается, если наблюдаемое значение критерия, принадлежит критической области, и не отвергается, если наблюдаемое значение принадлежит допустимой области.
Для проверки основной гипотезы используется специально подобранная случайная величина К, которая должна удовлетворять определенным требованиям(статический критерий):
ее закон распределения в случае истинности гипотезы должен быть известен.
характеризовать меру расхождения выборочных данных с основной гипотезой;
она должна являться функцией выборочных данных;
При проверке статистических гипотез всегда выдвигается две гипотезы:
Альтернативная (или конкурирующая) – гипотеза о различиях, обозначается H1. Она может быть ненаправленной и направленной.
Нулевая (или основная) – гипотеза о сходстве, обозначается H0.