da Cleiver Jiménez mancano 3 anni
226
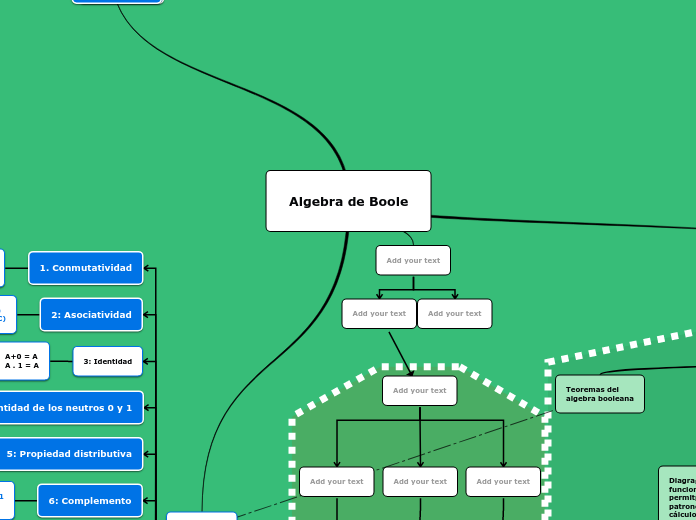
Algebra de Boole
El álgebra de Boole es fundamental en la simplificación de expresiones booleanas, utilizando diversas propiedades y teoremas que facilitan la manipulación de estas expresiones. Entre los métodos más destacados se encuentran el uso de Mapas de Karnaugh y el método de Quine-McCluskey.