DISTRIBUCIÓN NORMAL

Più simili a questo

Probabilidad simple

da xilene garizado

La Farmacocinética

da Hector Zambrano

Mapa de procesos en la red logistica

da Luis Enrique Gualguan

clinica 1

da LAURA CAMILA CAICEDO ORTEGA

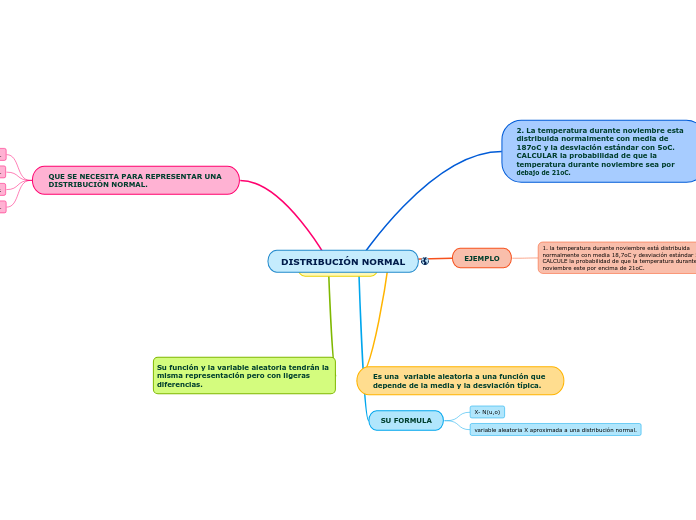
DISTRIBUCIÓN NORMAL

Su función y la variable aleatoria tendrán la misma representación pero con ligeras diferencias.

Topic principal

QUE SE NECESITA PARA REPRESENTAR UNA DISTRIBUCIÓN NORMAL.

calcular la desviación típica.

Decidir la función que queremos representar.

calcular la media.

UnA Variable aleatoria.

SU FORMULA

variable aleatoria X aproximada a una distribución normal.

X- N(u,o)

Es una variable aleatoria a una función que depende de la media y la desviación típica.

EJEMPLO

1. la temperatura durante noviembre está distribuida normalmente con media 18,7oC y desviación estándar 5oC. CALCULE la probabilidad de que la temperatura durante noviembre este por encima de 21oC.

la probabilidad de que ocurran temperaturas menores que 21oC es de 0,6772, entonces ahora la probabilidad de que ocurran temperaturas mayores será: 1- 06,772= 0,3228. esto es un 32.,28%

2. La temperatura durante noviembre esta distribuida normalmente con media de 187oC y la desviación estándar con 5oC. CALCULAR la probabilidad de que la temperatura durante noviembre sea por debajo de 21oC.

Sucesos menores que Z= 0,46 es lo mismo que decir que la temperatura sea menor que 21oC. Con la variable X hablamos de temperatura, con la variable estándar seria Z

Justamente, la tabla nos proporciona la probabilidad desde que ocurran sucesos menores que Z. Esto es, la probabilidad de que ocurran sucesos desde infinito hasta el valor de Z de 0,46 es 0,6772. Esto es un 67,72%.

u= 18,7°C o= 5°C X= 21°C

Z= X-u /o= 21-18, 7/5= 0,46

Ahora vamos a la tabla y para el valor de Z= 0,46 tenemos que la probabilidad es de 0,6772.