Ecuaciones Diferenciales - Transformada de Laplace - Mapa Conceptual

Più simili a questo

EL DIENCEFALO

da Valentina Vallecilla

POLICIA NACIONAL DEL PERU

da OMAR ASUNCION NAVARRO EGUSQUIZA

La preposición

da Luisamaria Garrido Aliaga

Las escuelas de mercadeo

da Daniela Acosta

Serie de Fourier

Funciones pares e impares una funcion y=g(x) es par si g(-x)=g(x) como lo es la funcion ncoseno que es simetrica con respecto del eje y. una funcion y=h(x) es impar si h(-x)=-h(x) como lo es la funcion seno porque no es simetrica al eje de las y. Si una funcion es par, entonces podemos decir que analizamos la mitad de su periodo, en conclusion si f(x) es par, el integrando del seno en la formula de an es impar y bn=0, de manera similar si f(x) es impar, entonces el integrando del seno de la formula bn es impar y an=0

Funciones periódicas Una función f(t) tiene un período T o es periódica con período T si para todo t, f(t+T)=f(t),para toda x, donde T es una constante positiva. El valor más pequeño de T>0 se llama el período principal o período fundamental o simplemente el período de f(t).

Las funciones senos y cosenos tienen una repeticion periodica en su grafica, en cualquier intervalo de longitud t, como asi tambien una funcion constante f=c, ya que satisface f(x+c)=f(x) para toda t>0, entonces se tiene que f(x+2t)=f((x+t)+t)= f(x+t)=f(x) y para cualquier n perteneciente a los naturales f(x+nt)=f(x) para toda x. Ademas si f(x) y g(x) tienen el mismo periodo, entonces la funcion h(x)=af(x)+bg(x). Si establecemos a t=2pi, entonces en terminos de funciones de senos y cosenos tenemos una serie de forma a0+a1cosx+b1senx+a2cosx+b2senx... donde los coeficientes a0,a1,b1... son constantes pertenecientes a los reales, y llamamos a esta serie, serie trigonometrica, y a los coeficientes an y bn, coeficientes de la serie.

Es una forma de representar funciones arbitrarias f(x) como la suma infinita de senos y cosenos, aumentando su frecuencia, relacionandolos armonicamente

Serie de Fourier Trigonometrica

Deduccion de los coeficientes

*seno de pi por cualquier numero es 0 *los senos me quedaran como cosenos reciprocos despues de evaluar la integral de bn

Calculo de bn

Calculo de an

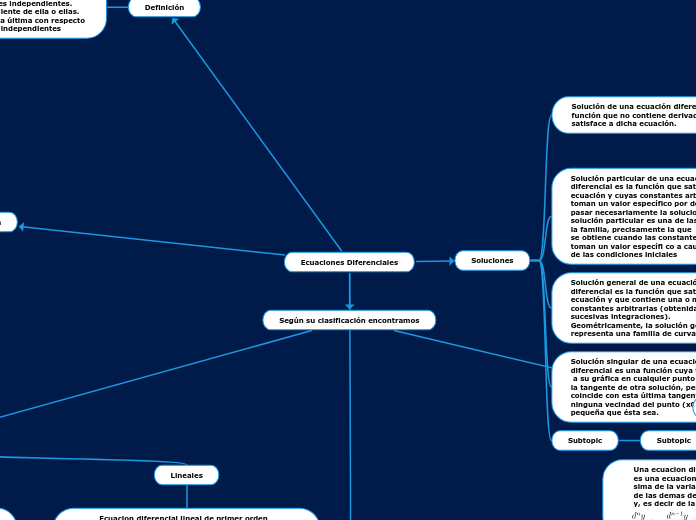
Ecuaciones Diferenciales

Según su clasificación encontramos

EDOS

Su solucion esta dada por

Y decimos que una solucion general consta de una solucion de la parte homogenea y de una solucion particular de la parte no homogenea y=yh+yp

Teorema de existencia y unicidad de soluciones para ecuaciones lineales de orden n

Dada la ecuacion diferencial lineal de orden n, siendo b(x),ai(x) con i=1,2,...n, funciones continuas en un intervalo (a,b). Si x0 es cualquier punto del intervalo y si y0,y'0,...y0^(n-1) son constantes arbitrarias, la ecuacion dada tiene una unica solucion en dicho intervalo, de forma que y(x0)=y0 y'(x0)=y'0 .... y^(n-1)(x0)=y0^(n-1)

Una ecuacion diferencial lineal de orden n, es una ecuacion en la que la derivada n-sima de la variable y es una funcion lineal de las demas derivadas de la propia funcion y, es decir de la forma:

Dependencia e independencia lineal

Dadas n funciones fi(x) con i=1,2,...n, son linealmente dependiente si existen constantes Ci pertenecientes a los reales, de forma tal que que la suma de la multiplicacion de las constantes por la funcion es igual a 0. Si existe Ci nulos, entonces se dice que las funciones son linealmente independientes

Si b(x)=/=0 es una Ecuacion lineal no homogenea

No Homogeneas

Superposicion de soluciones

Si tenemos una ecuacion lineal donde b(x)=/=0, y sea f1(x) una solucion particular =b1(x), y f2(x) otra solucion particular =b2(x), entonces f1(x) + f2(x) es solucion particular de la ecuacion. Es decir yp= B1x^2+B2x+C, donde tenemos que encontrar los coeficientes derivando y sustituyendo en la ecuacion original. Para esto utilizamos dos metodos

Metodo de variacion de parametros

Suponemos como solucion y=uy1+vy2, donde y1 e y2 son solucion de la ecuacion correspondiente, u y v tienen la forma u=integral(y2b(x)/W(y1y2) v=integral(y1b(x)/W(y1y2) por lo tanto yp=-y1integral(y2b(x)/W)+y2integral(y1b(x)/W)

Metodo de coeficientes indeterminados Caracteristicas de la ecuacion: *Coeficientes constantes *b(x) especiales

b(x)= Senos y cosenos

b(x) tiene la forma Kcos(wx) o Ksen(wx), entonces elegimos Kcos(wx)+Ksen(wx)

b(x)=Exponencial

b(x) tiene la forma de Ke^bx, y la funcion similar que debemos elegir es Ce^rx. Cuando una de las raices de la homogenea es igual al exponente de la funcion b(x), proponemos {a(e^rx)x}

b(x)=Polinomios

b(x) tienen la forma de Kx^n, donde n=(0,1,2...) Kx^n+ K(n-1)x^(n-1)+....K1x+K0. En caso de faltar el termino independiente se toma un polinomio de grado mayor

Si b(x)=0, entonces es una Ecuacion lineal homogenea

Partimos de que la solucion de una EDL de primer grado es y=Ce^-fx, el exponente puiede ser positivo dependiendo del valor de f, por lo que podemos igualar -f=m, entonces tambien tenemos en cuenta que podemos asumir que para las EDLOS la solucion tambien sera una exponencial, Sin tener en cuenta el valor de C reemplazamos y calculamos la derivada de la funcion: y=e^mx, y'=me^mx, y''=m^2e^mx. Reemplazamos en la EDLOS y tenemos que: a(m^2e^mx)+b(me^mx)+c(e^mx)=0 sacando factor comun: e^mx(am^2)+(bm)+(c)=0 Donde el resultado pueden ser 3 casos

3° caso: Raíces complejas

2° caso: Raíces iguales

1° caso: Raíces distintas

EDO

Ecuacion diferencial lineal de primer orden responde a la forma

Donde los coeficientes ai(x) son funciones reales y an(x)=/=0.

Una ecuacion de la forma y'+p(x)y=r(x)

Si r(x)=0, entonces es una ecuacion lineal homogenea, reducible a variables separables

Si r(x)=/= de 0, entonces es una ecuacion lineal no homogenea. Puede tratarse a esta ecuacion como una que admite un factor integrante de la forma (2). Despues se multiplican todos los terminos de la ecuacion por el resultado de la integracion del factor integrante, luego se identifica la derivada de un producto del factor integrante por la variable dependiente.

Exactas

Homogeneas

Una ecuacion de la forma M(x,y)dx+N(x,y)dy=0, es homogenea si M y N tienen la propiedad de que para toda t>0, la sustitucion de x=tx y la de y=ty, hacen que M y N sean del mismo grado M(tx,ty)= t^n M(x,y) - N(tx,ty)= t^n M(x,y) Luego de hacer la sustitucion, se reducen los terminos semejantes para llegar a una ecuacion que se resuelve por variables separables.

Variables separables

Una ecuacion de la forma dy/dx=g(x)/h(y), donde cada diferencial tiene como coeficiente una función de su propia variable, es separable si al separar la ecuacion en terminos de las variables x e y, e integrar los terminos de cada funcion h(y)dy=g(x)dx , se reduce a la ecuacion resultante de manera implicita

Soluciones

Subtopic

Solución singular de una ecuación diferencial es una función cuya tangente a su gráfica en cualquier punto (x0,y0) con la tangente de otra solución, pero ya no coincide con esta última tangente en ninguna vecindad del punto (x0,y0 ), por pequeña que ésta sea.

Solución general de una ecuación diferencial es la función que satisface a la ecuación y que contiene una o más constantes arbitrarias (obtenidas de las sucesivas integraciones). Geométricamente, la solución general representa una familia de curvas;

Solución particular de una ecuación diferencial es la función que satisface la ecuación y cuyas constantes arbitrarias toman un valor específico por donde debe pasar necesariamente la solucion.La solución particular es una de las curvas de la familia, precisamente la que se obtiene cuando las constantes arbitrarias toman un valor específi co a causa de las condiciones iniciales

Solución de una ecuación diferencial es una función que no contiene derivadas y que satisface a dicha ecuación.

Implicita: donde no se expresa de forma directa la relacion entre la variable dependiente e independiente.

Explicita: donde las variables dependientes se expresan tan solo en terminos de la variable independiente y constante.

Clasificación

Campo direccional: La idea fundamental del campo direccional es que la derivada de una función proporciona su pendiente. Al tratar con ecuaciones diferenciales se trabaja con expresiones en las que la derivada aparece como una variable

Dos curvas son ortogonales en un punto si, y sólo si, sus tangentes son perpendiculares en el punto de intersección. Trayectorias ortogonales son las curvas que se intersecan formando un ángulo recto. Si una familia de curvas tiene la ecuación F(x,y,y')= 0, la ecuación diferencial de las trayectorias ortogonales a ella es otra familia de la forma:F(x,y,(-1/y'))= 0

Grado

Se llama grado de una ecuación diferencial al exponente, si es número natural, al que está elevada la derivada de mayor orden que aparece en ella. Si esta derivada está elevada a un exponente no natural no es posible definir el grado de la ecuación.

No Lineales

Las que no cumplen las propiedades anteriores

Lineales

a) La variable dependiente y y todas sus derivadas son de primer grado. b) Cada coeficiente de y y sus derivadas depende solamente de la variable independiente x.

Orden

Se llama orden de una ecuación diferencial al orden de la mayor derivada que aparece en la ecuación.

Orden n (y^n)

Tercer orden (y''')

Segundo orden (y'')

Primer orden (y')

Tipo

Parciales

La ecuación diferencial contiene derivadas parciales de una o más variables dependientes con respecto a dos o más variables independientes

Ordinarias

La ecuación diferencial contiene derivadas de una o más variables dependientes con respecto a una sola variable independiente.

Definición

Llamamos ecuación diferencial a cualquier ecuación en la que aparecen relacionadas: – Una o varias variables independientes. – Una variable dependiente de ella o ellas. – Las derivadas de esta última con respecto a una o más variables independientes

Transformada de Laplace

Propiedades

T.de Derivadas

Si y'(t) es continua a trozos y de orden exponencial en el intervalo de 0 a infinito, entonces

T. de Integrales

tomando g(t)=1 en el teorema de convolucion tenemos que

Linealidad

si a y b son constantes

Teoremas

de Convolucion

si las funciones f y g son continuas por tramos desde 0 a infinito, entonces el producto especial denotado como f*g se define

de Traslacion sobre el eje s

Si k es un numero real y la transformada de f(t) existe, entonces (imagen), F(s-k) es la grafica de F(s) desplazada en el eje s por la cantidad |k|

Definicion

Sea f una funcion definida para t>=0, entonces se dice que la integral es la tranformada de Laplace de f(imagen), siempre que la integral converja, es decir que el limite en 1 existe, el resultado es una funcion de s, donde ademas tambien podemos destacar que la exponencial es el nucleo de la transformada.

Transformada Inversa

Si F(s) es la transformada de laplaces de f(t), entonces la transformada inversa de F(s) es F(t)

Condiciones suficientes

Las condiciones que garantizan a la transformada es que f sea continua por tramos y que f sea de orden exponencial C, entonces la transformada de f(t) existe para s>C